மாதிரி நிலையான விலகல் சூத்திரம் | கணக்கிடுவது எப்படி?
மாதிரி நிலையான விலகலைக் கணக்கிடுவதற்கான சூத்திரம்
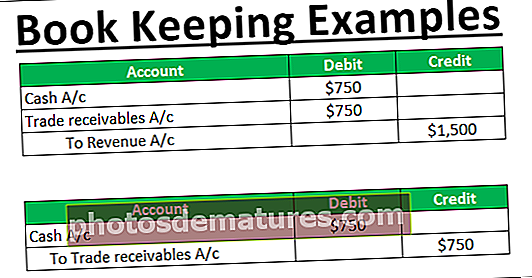
மாதிரி நிலையான விலகல் என்பது புள்ளிவிவர மெட்ரிக்கைக் குறிக்கிறது, இது மாதிரியின் சராசரியிலிருந்து ஒரு சீரற்ற மாறி எந்த அளவிற்கு மாறுபடுகிறது என்பதை அளவிட பயன்படுகிறது, மேலும் இது ஒவ்வொரு மாறியின் விலகலின் சதுரங்களையும் சராசரியிலிருந்து சேர்ப்பதன் மூலம் கணக்கிடப்படுகிறது, பின்னர் முடிவை பிரிக்கவும் பல மாறிகள் கழித்தல் மற்றும் முடிவின் எக்செல் இல் சதுர மூலத்தை கணக்கிடுகிறது.
கணித ரீதியாக, இது,
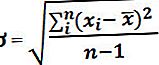
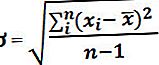
எங்கே
- எக்ஸ்நான் = ith சீரற்ற மாறி
- எக்ஸ் = மாதிரியின் சராசரி
- n = மாதிரியில் உள்ள மாறிகள் எண்ணிக்கை
மாதிரி நிலையான விலகலின் கணக்கீடு (படிப்படியாக)
- படி 1: முதலாவதாக, ஏராளமான மாறிகள் கொண்ட மக்கள்தொகையில் இருந்து சீரற்ற மாறிகள் சேகரிக்கவும். இந்த மாறிகள் ஒரு மாதிரியை உருவாக்கும். மாறிகள் x ஆல் குறிக்கப்படுகின்றனநான்.
- படி 2: அடுத்து, மாதிரியில் உள்ள மாறிகளின் எண்ணிக்கையைத் தீர்மானிக்கவும், அது n ஆல் குறிக்கப்படுகிறது.
- படி 3: அடுத்து, அனைத்து சீரற்ற மாறிகள் சேர்ப்பதன் மூலமும், மாதிரியில் உள்ள மாறிகளின் எண்ணிக்கையால் முடிவைப் பிரிப்பதன் மூலமும் மாதிரியின் சராசரியை தீர்மானிக்கவும். மாதிரி சராசரி x ஆல் குறிக்கப்படுகிறது.
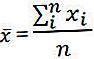
- படி 4: அடுத்து, மாதிரியின் ஒவ்வொரு மாறிக்கும் மாதிரி அர்த்தத்திற்கும் இடையிலான வேறுபாட்டைக் கணக்கிடுங்கள், அதாவது xநான் - எக்ஸ் .
- படி 5: அடுத்து, அனைத்து விலகல்களின் சதுரத்தைக் கணக்கிடுங்கள், அதாவது (xநான் - x) 2.
- படி 6: அடுத்து, ஸ்கொயர் விலகல்கள் அனைத்தையும் சேர்க்கவும், அதாவது ∑ (xநான் - x) 2.
- படி 7: அடுத்து, அனைத்து சதுர விலகல்களின் கூட்டுத்தொகையை மாதிரி கழித்தல் ஒன்றில் உள்ள மாறிகள் எண்ணிக்கையால் வகுக்கவும், அதாவது (n - 1).
- படி 8: இறுதியாக, மாதிரி நிலையான விலகலுக்கான சூத்திரம் மேலே காட்டப்பட்டுள்ள முடிவின் சதுர மூலத்தைக் கணக்கிடுவதன் மூலம் கணக்கிடப்படுகிறது.
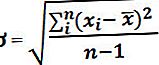
எடுத்துக்காட்டுகள்
இந்த மாதிரி நிலையான விலகல் ஃபார்முலா எக்செல் வார்ப்புருவை இங்கே பதிவிறக்கம் செய்யலாம் - மாதிரி நிலையான விலகல் ஃபார்முலா எக்செல் வார்ப்புருஎடுத்துக்காட்டு # 1
ஒவ்வொரு வாரமும் எத்தனை பென்சில்களைப் பயன்படுத்துகிறார்கள் என்பதைப் பார்க்க கணக்கெடுக்கப்பட்ட 5 மாணவர்களின் மாதிரியின் உதாரணத்தை எடுத்துக் கொள்வோம். கொடுக்கப்பட்ட பதில்களின் அடிப்படையில் மாதிரி நிலையான விலகலைக் கணக்கிடுங்கள்: 3, 2, 5, 6, 4
கொடுக்கப்பட்ட,
- மாதிரி அளவு (n) = 5
மாதிரி நிலையான விலகலைக் கணக்கிடுவதற்கான தரவு கீழே கொடுக்கப்பட்டுள்ளது.
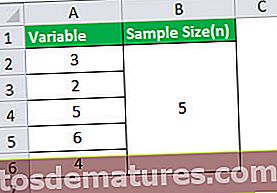
மாதிரி சராசரி
மாதிரி சராசரி கணக்கீடு
மாதிரி சராசரி = (3 + 2 + 5 + 6 + 4) / 5

மாதிரி சராசரி = 4
ஒவ்வொரு மாறியின் விலகல்களின் சதுரங்களை கீழே கணக்கிடலாம்,
- (3 – 4)2 = 1
- (2 – 4)2 = 4
- (5 – 4)2 = 1
- (6 – 4)2 = 4
- (4 – 4)2 = 0
இப்போது, மேலே உள்ள சூத்திரத்தைப் பயன்படுத்தி மாதிரி நிலையான விலகலைக் கணக்கிடலாம்,
- = √ {(1 + 4 + 1 + 4 + 0) / (5 - 1)}
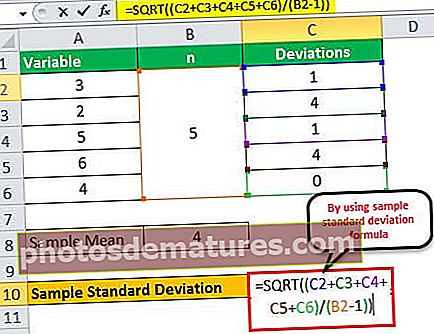
விலகல் இருக்கும் -
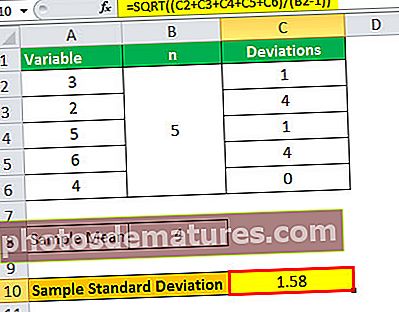
- = 1.58
எனவே, மாதிரி நிலையான விலகல் 1.58 ஆகும்.
எடுத்துக்காட்டு # 2
நியூயார்க்கில் சுமார் 5,000 பேர் பணிபுரியும் ஒரு அலுவலகத்தின் உதாரணத்தை எடுத்துக்கொள்வோம், உழைக்கும் மக்களின் சராசரி வயதை தீர்மானிக்க 10 பேரின் மாதிரியில் ஒரு கணக்கெடுப்பு மேற்கொள்ளப்பட்டுள்ளது. கொடுக்கப்பட்ட 10 பேரின் வயது அடிப்படையில் மாதிரி நிலையான விலகலை தீர்மானிக்கவும்: 23, 27, 33, 28, 21, 24, 36, 32, 29, 25
கொடுக்கப்பட்ட,
- மாதிரி அளவு (n) = 10
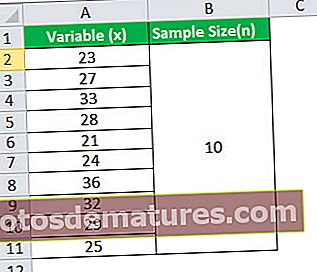
மேலே உள்ள தரவைப் பயன்படுத்துவதன் மூலம் முதலில் மாதிரி சராசரியைக் கணக்கிடுவோம்
மாதிரி சராசரி
மாதிரி சராசரி கணக்கீடு
= (23 + 27 + 33 + 28 + 21 + 24 + 36 + 32 + 29 + 25) / 10

மாதிரி சராசரி = 27.8
ஒவ்வொரு மாறியின் விலகல்களின் சதுரங்களை கீழே கணக்கிடலாம்,
- (23 – 27.8)2 = 23.04
- (27 – 27.8)2 = 0.64
- (33 – 27.8)2 = 27.04
- (28 – 27.8)2 = 0.04
- (21 – 27.8)2 = 46.24
- (24 – 27.8)2 = 14.44
- (36 – 27.8)2 = 67.24
- (32 – 27.8)2 = 17.64
- (29 – 27.8)2 = 1.44
- (25 – 27.8)2 = 7.84
விலகல்
இப்போது, மேலே உள்ள சூத்திரத்தைப் பயன்படுத்தி விலகலைக் கணக்கிடலாம்,
- ơ = √ {(23.04 + 0.64 + 27.04 + 0.04 + 46.24 +14.44 +67.24 + 17.64 + 1.44 + 7.84) / (10 - 1)}
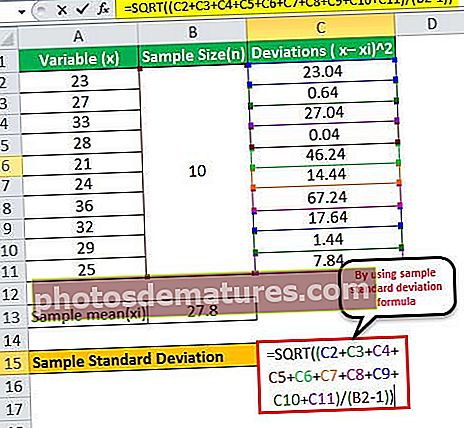
விலகல் இருக்கும் -
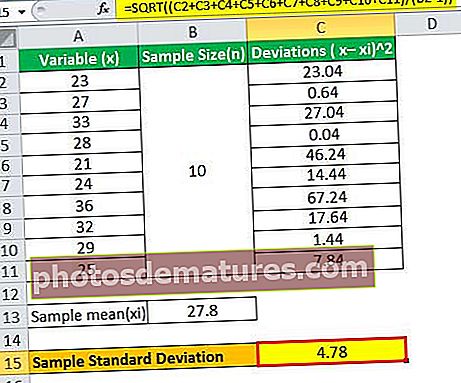
- = 4.78
விரிவான கணக்கீட்டைப் புரிந்து கொள்ள மேலே கொடுக்கப்பட்ட எக்செல் தாளை நீங்கள் குறிப்பிடலாம்.
சம்பந்தம் மற்றும் பயன்கள்
மாதிரி நிலையான விலகலின் கருத்து ஒரு புள்ளிவிவர நிபுணரின் பார்வையில் இருந்து மிகவும் முக்கியமானது, ஏனெனில் வழக்கமாக தரவுகளின் மாதிரி பெரிய மாறிகள் (மக்கள் தொகை) தொகுப்பிலிருந்து எடுக்கப்படுகிறது, இதிலிருந்து புள்ளிவிவரங்கள் முழு மக்களுக்கும் முடிவுகளை மதிப்பிட அல்லது பொதுமைப்படுத்த எதிர்பார்க்கப்படுகிறது. நிலையான விலகலின் அளவீடு இதற்கு விதிவிலக்கல்ல, எனவே, புள்ளிவிவர நிபுணர் வரையப்பட்ட மாதிரியின் அடிப்படையில் மக்கள்தொகை தரநிலை விலகலை மதிப்பீடு செய்ய வேண்டும், அங்குதான் அத்தகைய விலகல் செயல்பாட்டுக்கு வருகிறது.