photosdematures.com

பயனுள்ள வட்டி வீத வரையறை

பயனுள்ள வட்டி வீதம், வருடாந்திர சமமான வீதம் என்றும் அழைக்கப்படுகிறது, இது நிதிக் கருவியில் நபர் உண்மையில் செலுத்தும் அல்லது சம்பாதிக்கும் வட்டி வீதமாகும், இது அந்தக் காலப்பகுதியில் கூட்டுப்பணியின் விளைவைக் கருத்தில் கொண்டு கணக்கிடப்படுகிறது.

பயனுள்ள வட்டி வீத சூத்திரம்

பயனுள்ள வட்டி வீத சூத்திரம் = (1 + i / n) n -

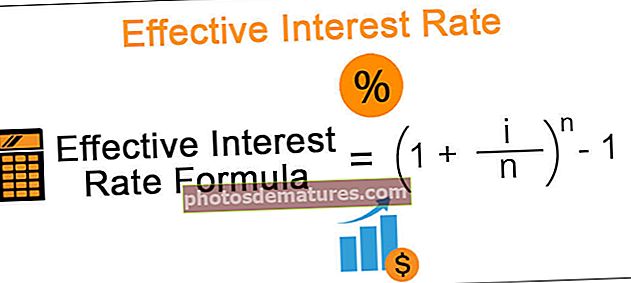
இங்கே, நான் = கருவியில் குறிப்பிடப்பட்டுள்ள வருடாந்திர வட்டி விகிதம்.

n = இது வருடத்திற்கு கூட்டு காலங்களின் எண்ணிக்கையைக் குறிக்கிறது.

விளக்கங்கள்

கூட்டு வட்டி விகிதத்தை மாற்றுகிறது. அதனால்தான் கருவியில் எழுதப்பட்ட வட்டி விகிதம் முதலீட்டாளருக்கு பயனுள்ள வட்டி விகிதம் (வருடாந்திர சமமான வீதம்) அல்ல. எடுத்துக்காட்டாக, கருவியில் 11% வட்டி விகிதம் எழுதப்பட்டு வட்டி விகிதம் ஆண்டுக்கு நான்கு முறை கூட்டப்பட்டால், வருடாந்திர சமமான விகிதம் 11% ஆக இருக்க முடியாது.

அது என்னவாக இருக்கும்?

அது - (1 + i / n) n - 1 = (1 + 0.11 / 4) 4 - 1 = 1.1123 - 1 = 0.1123 = 11.23%.

அதாவது 11.23% முதலீட்டாளருக்கு பயனுள்ள வட்டி விகிதமாக இருக்கும்.

மாற்றம் அற்பமானதாக இருந்தாலும், அது கருவியில் குறிப்பிடப்பட்டுள்ள வருடாந்திர வட்டி விகிதத்திற்கு சமமானதல்ல.

உதாரணமாக

எடுத்துக்காட்டு # 1

டிங் ஒரு குறிப்பிட்ட கருவியை வாங்கினார். கருவியில் குறிப்பிடப்பட்டுள்ள வட்டி விகிதம் 16% ஆகும். அவர் சுமார், 000 100,000 முதலீடு செய்துள்ளார். கருவி ஆண்டுதோறும் சேர்கிறது. இந்த குறிப்பிட்ட கருவியின் பயனுள்ள வட்டி விகிதம் (AER) என்னவாக இருக்கும்? ஒவ்வொரு ஆண்டும் அவர் வட்டியாக எவ்வளவு பெறுவார்?

பயனுள்ள வட்டி வீதமும் வருடாந்திர வீதமும் எப்போதும் ஒரே மாதிரியாக இருக்காது, ஏனெனில் வட்டி ஒவ்வொரு ஆண்டும் பல முறை கூட்டுகிறது. சில நேரங்களில், வட்டி விகிதம் அரை ஆண்டு, காலாண்டு அல்லது மாதாந்திரமாக அதிகரிக்கிறது. வருடாந்திர வட்டி விகிதத்திலிருந்து வருடாந்திர சமமான விகிதம் வேறுபடுகிறது.

இந்த எடுத்துக்காட்டு அதை உங்களுக்குக் காட்டுகிறது.

கணக்கிடுவோம்.

வட்டி விகிதம் ஆண்டுதோறும் ஒருங்கிணைக்கப்படுவதால், பயனுள்ள வட்டி வீத சூத்திரம் இங்கே இருக்கும் -

(1 + i / n) n - 1 = (1 + 0.16 / 1) 1 - 1 = 1.16 - 1 = 0.16 = 16%.

அதாவது இந்த குறிப்பிட்ட எடுத்துக்காட்டில், வருடாந்திர வட்டி வீதத்திற்கும் வருடாந்திர சமமான வீதத்திற்கும் (AER) எந்த வித்தியாசமும் இருக்காது.

ஒவ்வொரு ஆண்டும் டிங் கருவியில் = ($ 100,000 * 16%) = $ 16,000 வட்டி பெறுவார்.

எடுத்துக்காட்டு # 2

டோங் ஒரு குறிப்பிட்ட கருவியை வாங்கினார். கருவியில் குறிப்பிடப்பட்டுள்ள வட்டி விகிதம் 16% ஆகும். அவர் சுமார், 000 100,000 முதலீடு செய்துள்ளார். கருவி ஆண்டுக்கு ஆறு முறை கலக்கிறது. இந்த குறிப்பிட்ட கருவியின் வருடாந்திர சமமான வீதம் (AER) என்னவாக இருக்கும்? ஒவ்வொரு ஆண்டும் அவர் வட்டியாக எவ்வளவு பெறுவார்?

இது முந்தைய உதாரணத்தின் நீட்டிப்பு மட்டுமே.

ஆனால் மிகப்பெரிய வித்தியாசம் உள்ளது.

முந்தைய எடுத்துக்காட்டில், கருவி வருடத்திற்கு ஒரு முறை ஒருங்கிணைக்கப்பட்டது, இது வருடாந்திர வட்டி விகிதத்தை ஆண்டுக்கு சமமான விகிதத்திற்கு ஒத்ததாக மாற்றியது.

இருப்பினும், இந்த விஷயத்தில், காட்சி முற்றிலும் வேறுபட்டது.

வருடத்திற்கு ஆறு முறை கூட்டு வட்டி விகிதம் இங்கே உள்ளது.

எனவே, வருடாந்திர வட்டி வீதத்தின் சூத்திரம் இங்கே -

(1 + i / n) n - 1 = (1 + 0.16 / 6) 6 - 1 = 1.171 - 1 = 0.171 = 17.1%.

வட்டி விகிதம் வருடத்திற்கு ஆறு முறை கூட்டப்பட்டால், வருடாந்திர சமமான விகிதம் மிகவும் வித்தியாசமாக இருப்பதை நீங்கள் இப்போது காணலாம்.

இப்போது, ​​எங்களிடம் பயனுள்ள வட்டி விகிதம் இருப்பதால், இந்த ஆண்டின் இறுதியில் டோங் பெறும் வட்டி கணக்கிடலாம்.

டோங் = ($ 100,000 * 17.1%) = $ 17,100 கிடைக்கும்.

முந்தைய எடுத்துக்காட்டில் டிங் பெறும் வட்டி வட்டி விகிதங்கள் வித்தியாசமாக கலந்தால், டாங்கைப் பெறுவதை ஒப்பிட்டுப் பார்த்தால், வட்டிக்கு சுமார் 00 1100 வித்தியாசம் இருப்பதைக் காண்போம்.

எடுத்துக்காட்டு # 3

பிங் ஒரு கருவியில் முதலீடு செய்துள்ளார். அவர் $ 10,000 முதலீடு செய்துள்ளார். கருவியில் குறிப்பிடப்பட்டுள்ள வட்டி விகிதம் 18% ஆகும். வட்டி மாதந்தோறும் அதிகரிக்கும். முதல் ஆண்டில் பிங் ஒவ்வொரு மாதமும் எவ்வாறு வட்டி பெறுவார் என்பதைக் கண்டறியவும்.

வருடாந்திர சமமான வீதத்திற்கு இது மிகவும் விரிவான எடுத்துக்காட்டு.

இந்த எடுத்துக்காட்டில், பயனுள்ள வட்டி வீத சூத்திரத்தைப் பயன்படுத்தாமல் கணக்கீடு உண்மையில் எவ்வாறு நிகழ்கிறது என்பதைக் காண்பிப்போம்.

பார்ப்போம்.

வட்டி விகிதம் மாதந்தோறும் ஒருங்கிணைக்கப்படுவதால், மாதத்திற்கு குறிப்பிடப்பட்ட வட்டி வீதத்தின் உண்மையான முறிவு = (18/12) = 1.5% ஆகும்.

• முதல் மாதத்தில், பிங் = (10,000 * 1.5%) = $ 150 வட்டி பெறுவார்.
• இரண்டாவது மாதத்தில், பிங் = {(10,000 + 150) * 1.5%} = (10,150 * 1.5%) = $ 152.25 வட்டி பெறுவார்.
• மூன்றாவது மாதத்தில், பிங் = {(10,000 + 150 + 152.25) * 1.5%} = (10,302.25 * 1.5%) = $ 154.53 வட்டி பெறுவார்.
• நான்காவது மாதத்தில், பிங் = {(10,000 + 150 + 152.25 + 154.53) * 1.5%} = (10,456.78 * 1.5%) = $ 156.85 வட்டி பெறுவார்.
• ஐந்தாவது மாதத்தில், பிங் = {(10,000 + 150 + 152.25 + 154.53 + 156.85) * 1.5%} = (10,613.63 * 1.5%) = $ 159.20 வட்டி பெறுவார்.
• ஆறாவது மாதத்தில், பிங் = {(10,000 + 150 + 152.25 + 154.53 + 156.85 + 159.20) * 1.5%} = (10,772.83 * 1.5%) = $ 161.59 வட்டி பெறுவார்.
• ஏழாவது மாதத்தில், பிங் = {(10,000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59) * 1.5%} = (10,934.42 * 1.5%) = $ 164.02 வட்டி பெறுவார்.
• எட்டாவது மாதத்தில், பிங் = {(10,000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02) * 1.5%} = (11098.44 * 1.5%) = $ 166.48 வட்டி பெறுவார்.
• ஒன்பதாவது மாதத்தில், பிங் = {(10,000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02 + 166.48) * 1.5%} = (11264.92 * 1.5%) = $ 168.97 வட்டியைப் பெறுவார்.
• பத்தாவது மாதத்தில், பிங் = {(10,000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02 + 166.48 + 168.97) * 1.5%} = (11433.89 * 1.5%) = $ 171.51 வட்டி பெறுவார்.
• பதினொன்றாம் மாதத்தில், பிங் = {(10,000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02 + 166.48 + 168.97 + 171.51) * 1.5%} = (11605.40 * 1.5%) = $ 174.09 வட்டி பெறுவார்.
• பன்னிரண்டாம் மாதத்தில், பிங் = {(10,000 + 150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02 + 166.48 + 168.97 + 171.51 + 174.09) * 1.5%} = (11779.49 * 1.5%) = $ 176.69.

ஆண்டிற்கான பிங்கின் மொத்த வட்டி -

• (150 + 152.25 + 154.53 + 156.85 + 159.20 + 161.59 + 164.02 + 166.48 + 168.97 + 171.51 + 174.09 + 176.69) = $1956.18.

• வருடாந்திர சம விகித சூத்திரம் = (1 + i / n) n - 1 = (1 + 0.18 / 12) 12 - 1 = 1.195618 - 1 = 0.195618 = 19.5618%.

எனவே, வட்டி பிங் = ($ 10,000 ^ 19.5618%) = $ 1956.18 பெறும்.

எக்செல் இல் பயனுள்ள வட்டி விகிதம்

எக்செல் இல் பயனுள்ள வட்டி விகிதம் அல்லது வருடாந்திர சமமான விகிதத்தைக் கண்டறிய, எக்செல் செயல்பாட்டு EFFECT ஐப் பயன்படுத்துகிறோம்.

• பெயரளவு_ விகிதம் என்பது வட்டி வீதமாகும்
• nper என்பது வருடத்திற்கு கூட்டு காலங்களின் எண்ணிக்கை

கீழே உள்ள உதாரணத்தைப் பார்ப்போம்

• உங்களிடம் ஆண்டுதோறும் 10% பெயரளவு வட்டி விகிதம் இருந்தால், வருடாந்திர சம விகிதம் 10% ஆக இருக்கும்.
• ஆறு மாதங்களுக்கு 10% கூட்டு வட்டி விகிதம் உங்களிடம் இருந்தால், வருடாந்திர சமமான விகிதம் 10.25% ஆக இருக்கும்.
• உங்களிடம் காலாண்டுக்கு 10% கூட்டு வட்டி விகிதம் இருந்தால், வருடாந்திர சமமான விகிதம் 10.38% ஆக இருக்கும்.
• உங்களிடம் மாதந்தோறும் 10% கூட்டு வட்டி விகிதம் இருந்தால், வருடாந்திர சமமான விகிதம் 10.47% ஆக இருக்கும்.
• உங்களிடம் தினசரி 10% கூட்டு வட்டி விகிதம் இருந்தால், பயனுள்ள வட்டி விகிதம் 10.52% ஆக இருக்கும்.

பரிந்துரைக்கப்பட்ட வாசிப்புகள்

பயனுள்ள வட்டி வீதத்திற்கும் அதன் வரையறைக்கும் இது வழிகாட்டியாக இருந்தது. படிப்படியான கணக்கீடுகளுடன் பயனுள்ள வட்டி விகிதத்தின் சூத்திரத்தை இங்கே விவாதிக்கிறோம். மேலதிக கற்றல்களுக்கு, நீங்கள் பின்வரும் கட்டுரைகளைப் பார்க்கலாம்

• எதிர்மறை வட்டி வீத எடுத்துக்காட்டு
• பங்கேற்பு வீதத்தைக் கணக்கிடுங்கள்
• வேறுபாடுகள் - தள்ளுபடி விகிதம் மற்றும் வட்டி விகிதம்
• பெயரளவு வட்டி வீத சூத்திரம்
• ஒருங்கிணைப்பு
<