எக்செல் இல் சி ஸ்கொயர் டெஸ்ட் | எடுத்துக்காட்டுடன் சி ஸ்கொயர் டெஸ்ட் செய்வது எப்படி
எக்செல் உடன் சி-ஸ்கொயர் டெஸ்ட்
எக்செல் இல் சி-ஸ்கொயர் சோதனை என்பது தோராயமாக தேர்ந்தெடுக்கப்பட்ட தரவுகளுக்கு இரண்டு அல்லது அதற்கு மேற்பட்ட மாறிகளை ஒப்பிடுவதற்குப் பயன்படுத்தப்படும் பொதுவாக பயன்படுத்தப்படும் அளவுரு அல்லாத சோதனை ஆகும். இது இரண்டு அல்லது அதற்கு மேற்பட்ட மாறிகள் இடையேயான உறவைக் கண்டறியப் பயன்படும் ஒரு வகை சோதனை, இது சி-ஸ்கொயர் பி-மதிப்பு என்றும் அழைக்கப்படும் புள்ளிவிவரங்களில் பயன்படுத்தப்படுகிறது, எக்செல் இல் நமக்கு உள்ளடிக்கிய செயல்பாடு இல்லை, ஆனால் நாம் பயன்படுத்தலாம் சி-ஸ்கொயர் டெஸ்டுக்கான கணித சூத்திரத்தைப் பயன்படுத்தி எக்செல் இல் சி-சதுர சோதனையைச் செய்வதற்கான சூத்திரங்கள்.
வகைகள்
- பொருத்தத்தின் நன்மைக்காக சி-ஸ்கொயர் சோதனை
- இரண்டு மாறிகள் சுதந்திரத்திற்கான சி-சதுக்க சோதனை.
# 1 - பொருத்தத்தின் நன்மைக்கான சி-சதுக்க சோதனை
மக்கள்தொகைக்கு ஏற்ற மாதிரியின் அருகாமையை உணர இது பயன்படுத்தப்படுகிறது. சி-சதுக்க சோதனையின் சின்னம் (2). இது அனைவரின் கூட்டுத்தொகை (கவனிக்கப்பட்ட எண்ணிக்கை - எதிர்பார்க்கப்பட்ட எண்ணிக்கை) 2 / எதிர்பார்க்கப்பட்ட எண்ணிக்கை.
- k-1 டிகிரி சுதந்திரம் அல்லது DF.
- எங்கே ஓய் கவனிக்கப்பட்ட அதிர்வெண், கே பிரிவுகள், மற்றும் Ei எதிர்பார்த்த அதிர்வெண்.
குறிப்பு:- ஒரு புள்ளிவிவர மாதிரியின் பொருத்தத்தின் நன்மை என்பது மாதிரி தரவு அவதானிப்புகளின் தொகுப்பிற்கு எவ்வளவு பொருந்துகிறது என்பதைப் புரிந்துகொள்வதைக் குறிக்கிறது.
பயன்கள்
- கடன் பெறுபவர்களின் வயது மற்றும் தனிப்பட்ட கடன்களின் அடிப்படையில் கடன் மதிப்பு
- விற்பனையாளர்களின் செயல்திறனுக்கும் பெறப்பட்ட பயிற்சிக்கும் உள்ள தொடர்பு
- ஒரு பங்கு மற்றும் மருந்து அல்லது வங்கி போன்ற ஒரு துறையின் பங்குகளில் திரும்பவும்
- பார்வையாளர்களின் வகை மற்றும் தொலைக்காட்சி பிரச்சாரத்தின் தாக்கம்.
# 2 - இரண்டு மாறிகள் சுதந்திரத்திற்கான சி-சதுக்க சோதனை
மாறிகள் ஒருவருக்கொருவர் தன்னாட்சி கொண்டதா இல்லையா என்பதை சரிபார்க்க இது பயன்படுத்தப்படுகிறது. (R-1) (c-1) டிகிரி சுதந்திரத்துடன்
எங்கே ஓய் கவனிக்கப்பட்ட அதிர்வெண், r வரிசைகளின் எண்ணிக்கை, சி நெடுவரிசைகளின் எண்ணிக்கை, மற்றும் Ei எதிர்பார்த்த அதிர்வெண்
குறிப்பு:- ஒரு மாறியின் நிகழ்தகவு விநியோகம் மற்றொன்றால் பாதிக்கப்படாவிட்டால் இரண்டு சீரற்ற மாறிகள் சுயாதீனமாக அழைக்கப்படுகின்றன.பயன்கள்
சுதந்திர சோதனை பின்வரும் சூழ்நிலைகளுக்கு ஏற்றது:
- ஒரு வகை மாறிலி உள்ளது.
- இரண்டு வகைப்படுத்தப்பட்ட மாறிகள் உள்ளன, அவற்றுக்கு இடையிலான உறவை நீங்கள் தீர்மானிக்க வேண்டும்.
- குறுக்கு-அட்டவணைகள் உள்ளன, மேலும் இரண்டு வகை மாறிகளுக்கிடையேயான தொடர்பைக் கண்டறிய வேண்டும்.
- அளவிட முடியாத மாறிகள் உள்ளன (எடுத்துக்காட்டாக, வெவ்வேறு வயதினருக்கான ஊழியர்கள் வெவ்வேறு வகையான சுகாதாரத் திட்டங்களைத் தேர்வு செய்கிறார்களா?) போன்ற கேள்விகளுக்கான பதில்கள்.
எக்செல் இல் சி-ஸ்கொயர் டெஸ்ட் செய்வது எப்படி? (எடுத்துக்காட்டுடன்)
இந்த சி ஸ்கொயர் டெஸ்ட் எக்செல் வார்ப்புருவை இங்கே பதிவிறக்கம் செய்யலாம் - சி ஸ்கொயர் டெஸ்ட் எக்செல் வார்ப்புருஒரு உணவகத்தின் மேலாளர் வாடிக்கையாளர் திருப்திக்கும் அட்டவணைகளுக்காகக் காத்திருக்கும் மக்களின் சம்பளத்திற்கும் இடையிலான உறவைக் கண்டுபிடிக்க விரும்புகிறார். இதில், சி-சதுக்கத்தை சோதிக்க கருதுகோளை அமைப்போம்
- 100 வாடிக்கையாளர்களின் சீரற்ற மாதிரியை அவர் எடுத்துக்கொள்கிறார், இந்த சேவை சிறந்ததா, நல்லதா அல்லது மோசமானதா என்று கேட்கிறது.
- பின்னர் அவர் காத்திருக்கும் மக்களின் சம்பளத்தை குறைந்த, நடுத்தர மற்றும் உயர் என வகைப்படுத்துகிறார்.
- முக்கியத்துவத்தின் நிலை 0.05 என்று வைத்துக் கொள்ளுங்கள். இங்கே, H0 மற்றும் H1 ஆகியவை அட்டவணைகள் காத்திருக்கும் மக்களின் சம்பளத்தில் சேவை தரத்தின் சுதந்திரத்தையும் சார்புகளையும் குறிக்கின்றன.
- எச்0 - சேவைத் தரம் அட்டவணைகளுக்காகக் காத்திருக்கும் மக்களின் சம்பளத்தைப் பொறுத்தது அல்ல.
- எச்1 - சேவை தரம் அட்டவணைகளுக்காக காத்திருக்கும் மக்களின் சம்பளத்தைப் பொறுத்தது
- அவரது கண்டுபிடிப்புகள் கீழே உள்ள அட்டவணையில் காட்டப்பட்டுள்ளன:
இதில், எங்களிடம் 9 தரவு புள்ளிகள் உள்ளன, அவற்றில் 3 குழுக்கள் உள்ளன, அவை ஒவ்வொன்றும் சம்பளத்தைப் பற்றி வேறுபட்ட செய்தியைப் பெற்றன, இதன் விளைவு கீழே கொடுக்கப்பட்டுள்ளது.

இப்போது நாம் அனைத்து வரிசைகள் மற்றும் நெடுவரிசைகளின் கூட்டுத்தொகையை எண்ணப் போகிறோம். சூத்திரத்தின் உதவியுடன் இதைச் செய்வோம், அதாவது. SUM. நாங்கள் எழுதிய மொத்த நெடுவரிசையில் சிறந்ததை மொத்தமாக்க = SUM (B4: D4) பின்னர் Enter ஐ அழுத்தவும்.

இது நமக்குத் தரும் 26. எல்லா வரிசைகள் மற்றும் நெடுவரிசைகளிலும் நாங்கள் ஒரே மாதிரியாக செயல்படுவோம்.

கணக்கிட சுதந்திர பட்டம் (டி.எஃப்) நாம் பயன்படுத்த (r-1) (c-1)
டி.எஃப் = (3-1)(3-1)=2*2=4
- 3 வகை சேவை மற்றும் 3 வகை சம்பளம் உள்ளன
- நடுத்தர சம்பளத்துடன் (கீழ் வரிசை, நடுத்தர) 27 பதிலளித்தவர்கள் எங்களிடம் உள்ளனர்
- நல்ல சேவையுடன் 51 பதிலளித்தவர்கள் எங்களிடம் உள்ளனர் (கடைசி நெடுவரிசை, நடுத்தர)
இப்போது நாம் கணக்கிட வேண்டும் எதிர்பார்க்கப்படும் அதிர்வெண்கள்: -
எதிர்பார்க்கப்படும் அதிர்வெண்கள் ஒரு சூத்திரத்தைப் பயன்படுத்தி கணக்கிடலாம்: -
- கணக்கிட அருமை மொத்தத்தை பெருக்கி பயன்படுத்துவோம் குறைந்த மொத்தத்துடன் சிறந்த பிரிக்கப்பட்டுள்ளது வழங்கியவர் என்.
1 வது வரிசை மற்றும் 1 வது நெடுவரிசைக்கு நாம் கணக்கிட வேண்டும் என்று வைத்துக்கொள்வோம் (= பி 7 * இ 4 / பி 9). இது வாக்களித்த வாடிக்கையாளர்களின் எண்ணிக்கையை வழங்கும் அருமை காத்திருக்கும் மக்களின் சம்பளத்திற்கான சேவை குறைந்த அதாவது 8.32.
- இ11=(32*26)/100 = 8.32, இ12 = 7.02, இ13 = 10.66
- இ21 = 16.32, இ22 = 13.77, இ23 = 20.91
- இ31 = 7.36, இ32 = 6.21, இ33 = 9.41
அனைவருக்கும் இதேபோல், நாம் அதையே செய்ய வேண்டும் மற்றும் சூத்திரம் கீழே உள்ள வரைபடத்தில் பயன்படுத்தப்படுகிறது.

கீழே கொடுக்கப்பட்டுள்ளபடி எதிர்பார்க்கப்படும் அதிர்வெண் அட்டவணையைப் பெறுகிறோம்: -

குறிப்பு:- முக்கியத்துவத்தின் நிலை 0.05 என்று வைத்துக் கொள்ளுங்கள். இங்கே, H0 மற்றும் H1 ஆகியவை அட்டவணைகள் காத்திருக்கும் மக்களின் சம்பளத்தில் சேவை தரத்தின் சுதந்திரத்தையும் சார்புகளையும் குறிக்கின்றன.
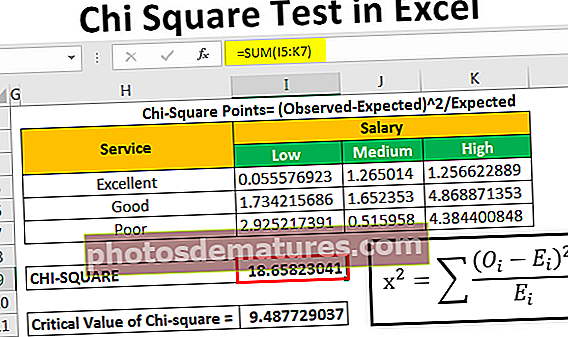
எதிர்பார்த்த அதிர்வெண்ணைக் கணக்கிட்ட பிறகு, ஒரு சூத்திரத்தைப் பயன்படுத்தி சி-சதுர தரவு புள்ளிகளைக் கணக்கிடுவோம்
சி-சதுர புள்ளிகள் = (கவனிக்கப்பட்ட-எதிர்பார்க்கப்பட்ட) ^ 2 / எதிர்பார்க்கப்படுகிறது
நாம் எழுதும் முதல் புள்ளியைக் கணக்கிட = (பி 4-பி 14) ^ 2 / பி 14.

மதிப்பை தானாக நிரப்ப சூத்திரத்தை மற்ற கலங்களில் நகலெடுத்து ஒட்டுவோம்.

இதற்குப் பிறகு, நாம் கணக்கிடுவோம் chi-value (கணக்கிடப்பட்ட மதிப்பு) அட்டவணைக்கு மேலே கொடுக்கப்பட்ட அனைத்து மதிப்புகளையும் சேர்ப்பதன் மூலம்

எங்களுக்கு சி-மதிப்பு கிடைத்தது 18.65823.

இதற்கான முக்கியமான மதிப்பைக் கணக்கிட, நாம் ஒரு சி-சதுர விமர்சன மதிப்பு அட்டவணையைப் பயன்படுத்துகிறோம், கீழே கொடுக்கப்பட்டுள்ள சூத்திரத்தைப் பயன்படுத்தலாம்.
இந்த சூத்திரத்தில் 2 அளவுருக்கள் உள்ளன CHISQ.INV.RT (நிகழ்தகவு, சுதந்திரத்தின் அளவு).
நிகழ்தகவு 0.05 ஆகும், இது ஒரு குறிப்பிடத்தக்க மதிப்பு, இது ஏற்றுக்கொள்வதா என்பதை தீர்மானிக்க எங்களுக்கு உதவும் பூஜ்ய கருதுகோள் (எச்0) அல்லது இல்லை.

சி-சதுரத்தின் முக்கியமான மதிப்பு 9.487729037.

இப்போது நாம் அதன் மதிப்பைக் காண்போம் chi-square அல்லது (P மதிப்பு)= CHITEST (உண்மையான_அரேஞ்ச், எதிர்பார்க்கப்பட்ட_அரேஞ்ச்)
வரம்பு = CHITEST (பி 4: டி 6, பி 14: டி 16).

சி-டெஸ்ட் அல்லது பி-மதிப்பின் மதிப்பு = 0.00091723 என்பதை நாம் பார்த்தோம்.

எல்லா மதிப்புகளையும் கணக்கிட்டுள்ளோம். தி chi-square (கணக்கிடப்பட்ட மதிப்பு) மதிப்புகள் அதன் மதிப்பு ஒன்று அல்லது அதற்கு மேற்பட்டதாக இருக்கும்போது மட்டுமே குறிப்பிடத்தக்கவை முக்கியமான மதிப்பு 9.48, அதாவது. முக்கியமான மதிப்பு (அட்டவணைப்படுத்தப்பட்ட மதிப்பு) விட அதிகமாக இருக்க வேண்டும் 18.65 ஏற்றுக்கொள்ள பூஜ்ய கருதுகோள் (எச்0).
ஆனால் இங்கே கணக்கிடப்பட்ட மதிப்பு >அட்டவணைப்படுத்தப்பட்ட மதிப்பு
எக்ஸ் 2 (கணக்கிடப்பட்டது)> எக்ஸ் 2 (அட்டவணைப்படுத்தப்பட்டுள்ளது)
18.65>9.48
இந்த வழக்கில், நாங்கள் நிராகரிப்போம் பூஜ்ய கருதுகோள் (எச்0) மற்றும் மாற்று (எச்1) ஏற்றுக்கொள்ளப்படும்.
- அதையும் கணிக்க பி-மதிப்பைப் பயன்படுத்தலாம், அதாவது பி-மதிப்பு <= α (குறிப்பிடத்தக்க மதிப்பு 0.05), பூஜ்ய கருதுகோள் நிராகரிக்கப்படும்
- என்றால் பி-மதிப்பு> α, வேண்டாம் நிராகரிக்க பூஜ்ய கருதுகோள்.
இங்கே பி-மதிப்பு (0.0009172)< α (0.05), எச் நிராகரிக்கவும்0, எச்1
மேலே உள்ள எடுத்துக்காட்டில் இருந்து, சேவை தரம் காத்திருக்கும் மக்களின் சம்பளத்தைப் பொறுத்தது என்று முடிவு செய்கிறோம்.
நினைவில் கொள்ள வேண்டிய விஷயங்கள்
- நிலையான இயல்பான மாறுபாட்டின் சதுரத்தைக் கருதுகிறது.
- வெவ்வேறு வகைகளில் காணப்பட்ட அதிர்வெண்கள் ஒரு குறிப்பிட்ட அனுமானங்களின் கீழ் எதிர்பார்க்கப்படும் அதிர்வெண்களிலிருந்து கணிசமாக வேறுபடுகின்றனவா என்பதை மதிப்பீடு செய்கிறது.
- கருதப்பட்ட விநியோகம் தரவுக்கு எவ்வளவு பொருந்துகிறது என்பதை தீர்மானிக்கிறது.
- தற்செயல் அட்டவணையைப் பயன்படுத்துகிறது (சந்தை ஆராய்ச்சிகளில், இந்த அட்டவணைகள் குறுக்கு தாவல்கள் என்று அழைக்கப்படுகின்றன).
- பெயரளவு அளவிலான அளவீடுகளை ஆதரிக்கிறது.