photosdematures.com

இடைக்கணிப்பு என்றால் என்ன?

எளிமையான சொற்களில் ஒரு குறிப்பிட்ட மதிப்பைக் கொண்ட இரண்டு புள்ளிகளுக்கு இடையில் மதிப்பைப் பெறுவதற்காகப் பயன்படுத்தப்படும் கணித நடைமுறை என இடைக்கணிப்பு விவரிக்கப்படலாம், கொடுக்கப்பட்ட தனித்துவமான புள்ளிகளின் தொகுப்பில் கொடுக்கப்பட்ட செயல்பாட்டின் மதிப்பை தோராயமாக மதிப்பிடும் செயல்முறையாக இதை விவரிக்கலாம். செலவு, கணிதம், புள்ளிவிவரம் போன்ற பல்வேறு கருத்துக்களை மதிப்பிடுவதில் இதைப் பயன்படுத்தலாம்.

அறியப்பட்ட மதிப்புகள் கொண்ட எந்தவொரு செயல்பாட்டிற்கும் அறியப்படாத மதிப்பை நிர்ணயிக்கும் முறையாக இடைக்கணிப்பு என்று கூறலாம். அறியப்படாத மதிப்பு கண்டுபிடிக்கப்பட்டது. கொடுக்கப்பட்ட மதிப்புகள் ஒரு நேரியல் போக்கில் செயல்பட்டால், அறியப்பட்ட இரண்டு புள்ளிகளிலிருந்து அறியப்படாத மதிப்பைத் தீர்மானிக்க எக்செல் இல் நேரியல் இடைக்கணிப்பு விண்ணப்பிக்கலாம்.

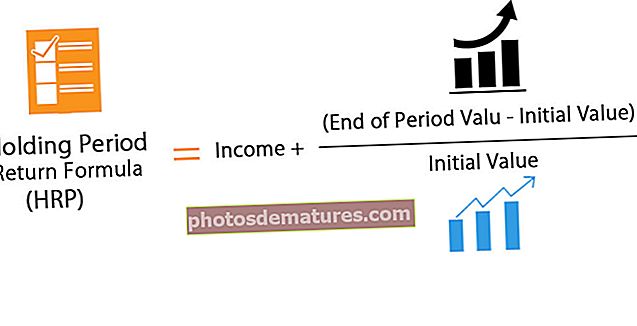
இடைக்கணிப்பு சூத்திரம்

சூத்திரம் பின்வருமாறு: -

மேலே குறிப்பிட்டுள்ள வரையறையில் நாம் கற்றுக்கொண்டது போல, மேலே உள்ள சூத்திரத்தில், மற்ற மதிப்புகளின் அடிப்படையில் ஒரு மதிப்பைக் கண்டறிய இது உதவுகிறது: -

• எக்ஸ் மற்றும் ஒய் அறியப்படாத புள்ளிவிவரங்கள், அவை கொடுக்கப்பட்ட பிற மதிப்புகளின் அடிப்படையில் கண்டறியப்படும்.
• Y1, Y2, X1 மற்றும் X2 ஆகியவை அறியப்படாத மதிப்பை தீர்மானிக்க உதவும் மாறிகளின் தொகுப்புகள் வழங்கப்படுகின்றன.

எடுத்துக்காட்டாக, மா மரங்களை வளர்ப்பதில் ஈடுபட்டுள்ள ஒரு விவசாயி குறிப்பிட்ட நாட்களில் மரத்தின் உயரம் குறித்து பின்வரும் தரவுகளை கவனித்து சேகரிக்கிறார்: -

கொடுக்கப்பட்ட தரவுத் தொகுப்பின் அடிப்படையில் விவசாயி மரம் அதன் சாதாரண உயரத்தை அடையும் வரை எத்தனை நாட்களுக்கு மரங்களின் உயரத்தை மதிப்பிட முடியும். மேற்கண்ட தரவுகளின் அடிப்படையில், விவசாயி மரத்தின் உயரத்தை 7 வது நாளில் தெரிந்து கொள்ள விரும்புகிறார்.

மேற்கண்ட மதிப்புகளை இடைக்கணிப்பதன் மூலம் அவர் அதைக் கண்டுபிடிக்க முடியும். 7 வது நாளில் மரத்தின் உயரம் 70 எம்.எம்.

இடைக்கணிப்புக்கான எடுத்துக்காட்டுகள்

இப்போது, ​​சில எளிய மற்றும் நடைமுறை எடுத்துக்காட்டுகளின் உதவியுடன் கருத்தை புரிந்துகொள்வோம்.

இந்த இடைக்கணிப்பு ஃபார்முலா எக்செல் வார்ப்புருவை இங்கே பதிவிறக்கம் செய்யலாம் - இடைக்கணிப்பு ஃபார்முலா எக்செல் வார்ப்புரு

எடுத்துக்காட்டு # 1

கொடுக்கப்பட்ட தரவுகளின் தொகுப்பிலிருந்து இடைக்கணிப்பு சூத்திரத்தைப் பயன்படுத்தி அறியப்படாத மதிப்பைக் கணக்கிடுங்கள். எக்ஸ் மதிப்பு 60 ஆக இருக்கும்போது Y இன் மதிப்பைக் கணக்கிடுங்கள்.

தீர்வு:

எக்ஸ் 60 ஆக இருக்கும்போது Y இன் மதிப்பை இன்டர்போலேஷன் உதவியுடன் பின்வருமாறு பெறலாம்: -

இங்கே எக்ஸ் 60, ஒய் தீர்மானிக்க வேண்டும். மேலும்,

எனவே, இடைக்கணிப்பின் கணக்கீடு இருக்கும் -

• Y = Y1 + (Y2-Y1) / (X2-X1) * (X-X1)
• =80 + (120-80)/(70-50) * (60-50)
• =80 + 40/20 *10
• = 80+ 2*10
• =80+20

• ஒய் = 100

எடுத்துக்காட்டு # 2

திரு. ஹாரி விற்பனை மற்றும் இலாப விவரங்களை பகிர்ந்து கொள்கிறார். விற்பனை எண்ணிக்கை, 75,00,000 ஐ எட்டும்போது அவர் தனது வணிகத்தின் லாபத்தை அறிய ஆர்வமாக உள்ளார். கொடுக்கப்பட்ட தரவின் அடிப்படையில் நீங்கள் லாபத்தை கணக்கிட வேண்டும்:

தீர்வு:

மேற்கண்ட தரவுகளின் அடிப்படையில், திரு. ஹாரியின் இலாபத்தை சூத்திரத்தைப் பயன்படுத்தி பின்வருமாறு மதிப்பிடலாம்:

இங்கே

எனவே, இடைக்கணிப்பின் கணக்கீடு இருக்கும் -

• Y = Y1 + (Y2-Y1) / (X2-X1) * (X-X1)
• = $ 5,00,000 + ($6,00,000 – $5,00,000)/($50,00,000 – $40,00,000) * ($75,00,000 – $40,00,000)
• = $ 5,00,000 + $1,00,000 / $10,00,000 * $ 35,00,000
• = $5,00,000 + $ 3,50,000

• ஒய் = $ 8,50,000

எடுத்துக்காட்டு # 3

திரு. லார்க் உற்பத்தி மற்றும் செலவுகள் பற்றிய விவரங்களைப் பகிர்ந்து கொள்கிறார். உலகளாவிய மந்தநிலை அச்சங்களின் இந்த சகாப்தத்தில், திரு. லார்க் தனது தயாரிப்பின் கோரிக்கைகளை குறைப்பார் என்ற அச்சத்தையும், தனது வணிகத்தின் மொத்த செலவை ஈடுசெய்ய உகந்த உற்பத்தி அளவை அறிய ஆர்வமாக உள்ளார். கொடுக்கப்பட்ட தரவின் அடிப்படையில் உற்பத்தியின் உகந்த அளவு அளவை நீங்கள் கணக்கிட வேண்டும். 90,00,000 டாலர் மதிப்பிடப்பட்ட செலவை ஈடுசெய்ய தேவையான உற்பத்தியின் அளவை தீர்மானிக்க லார்க் விரும்புகிறார்.

தீர்வு:

மேற்கண்ட தரவுகளின் அடிப்படையில், இடைக்கணிப்பு சூத்திரத்தைப் பயன்படுத்தி, 90,00,00 செலவை ஈடுகட்ட தேவையான அளவை நாம் பின்வருமாறு மதிப்பிடலாம்:

இங்கே,

Y = Y1 + (Y2-Y1) / (X2-X1) * (X-X1)

தேவையான உற்பத்தியின் அளவைப் பெற மேற்கண்ட சூத்திரத்தை பின்வருமாறு மாற்றியமைத்துள்ளோம்

X = (Y - Y1) / [(Y2-Y1) / (X2-X1)] + X1

• எக்ஸ் = (9,000,000 - 5,500,000) / [(6,000,000 - 5,500,000) / (500,000 - 400,000)] + 400,000
• = 3,500,000 /(5,00,000/1,00,000) + 400,000
• = 3,500,000 /5 + 400,000
• = 7,00,000 + 400,000
• = 11,00,000 அலகுகள்

இடைக்கணிப்பு கால்குலேட்டர்

நீங்கள் பின்வரும் கால்குலேட்டரைப் பயன்படுத்தலாம்.

எக்ஸ்
எக்ஸ் 1
எக்ஸ் 2
ஒய் 1
ஒய் 2
இடைக்கணிப்பு சூத்திரம்

இடைக்கணிப்பு சூத்திரம் =	Y1 + (Y2 - Y1) / (X2 - X1) * (X - X1)
	0 + ( 0 - 0 )/( 0 - 0 ) * ( 0 - 0 ) =	0

சம்பந்தம் மற்றும் பயன்பாடு

ஒவ்வொரு வணிகத்திலும் தரவு பகுப்பாய்வு முக்கிய பங்கு வகிக்கும் சகாப்தத்தில், அறியப்பட்ட மதிப்புகளின் தொகுப்பிலிருந்து வெவ்வேறு மதிப்புகளை மதிப்பிடுவதற்கு ஒரு அமைப்பு இடைக்கணிப்பைப் பயன்படுத்துகிறது. இடைக்கணிப்பின் சில பொருத்தங்கள் மற்றும் பயன்பாடுகள் கீழே குறிப்பிடப்பட்டுள்ளன.

• கொடுக்கப்பட்ட மூல மதிப்புகளின் தொகுப்பிலிருந்து அர்த்தமுள்ள முடிவுகளை பகுப்பாய்வு செய்ய மற்றும் பெற தரவு விஞ்ஞானிகளால் இடைக்கணிப்பு பயன்படுத்தப்படலாம்.
• விற்கப்பட்ட பொருட்களின் விலை, சம்பாதித்த இலாபங்கள் போன்ற ஒரு குறிப்பிட்ட செயல்பாட்டின் அடிப்படையில் அமைந்துள்ள எந்தவொரு நிதி தகவலையும் தீர்மானிக்க ஒரு நிறுவனத்தால் இதைப் பயன்படுத்தலாம்.
• அர்த்தமுள்ள தகவல்களைப் பெற ஏராளமான புள்ளிவிவர நடவடிக்கைகளில் இடைக்கணிப்பு பயன்படுத்தப்படுகிறது.
• பல மதிப்பீடுகளில் சாத்தியமான முடிவுகளை தீர்மானிக்க விஞ்ஞானிகளால் இது பயன்படுத்தப்படுகிறது.
• மூல சேகரிக்கப்பட்ட தரவுகளிலிருந்து பயனுள்ள தகவல்களைத் தீர்மானிக்க இந்த கருத்தை ஒரு புகைப்படக்காரரும் பயன்படுத்தலாம்.