சராசரி ஃபார்முலா | சராசரியைக் கணக்கிடுவது எப்படி? (படி படியாக)
சராசரியைக் கணக்கிட சூத்திரம்
சராசரி என்பது தரவுகளின் மதிப்புகளின் தொகுப்பைக் குறிக்கப் பயன்படும் மதிப்பு, இது முழு தரவிலிருந்து கணக்கிடப்பட்ட சராசரி மற்றும் கொடுக்கப்பட்ட தொகுப்பின் அனைத்து மதிப்புகளையும் சேர்ப்பதன் மூலம் இந்த சூத்திரம் கணக்கிடப்படுகிறது, இது X இன் சுருக்கத்தால் குறிக்கப்படுகிறது மற்றும் அதை எண்ணிக்கையால் வகுக்கிறது N ஆல் குறிக்கப்பட்ட தொகுப்பில் கொடுக்கப்பட்ட மதிப்புகள்.
சராசரி = (அ1 + அ2 +…. + அn) / n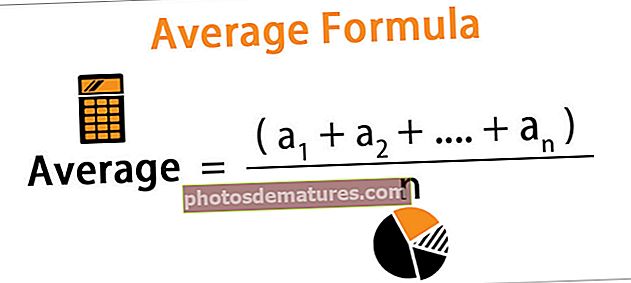
- எங்கேநான் = ith கவனிப்பு
- n = அவதானிப்புகள் எண்ணிக்கை
விளக்கம்
பின்வரும் படிகளைப் பயன்படுத்தி சராசரியின் கணக்கீட்டைக் கணக்கிடலாம்:
- படி 1: முதலாவதாக, கவனிப்பைத் தீர்மானியுங்கள், அவை a ஆல் குறிக்கப்படுகின்றன1, அ2,… .., அn 1 வது அவதானிப்பு, 2 வது கண்காணிப்பு,…., n வது கண்காணிப்பு.
- படி 2: அடுத்து, அவதானிப்புகளின் எண்ணிக்கையைத் தீர்மானிக்கவும், அது n ஆல் குறிக்கப்படுகிறது.
- படி 3: இறுதியாக, சராசரி அனைத்து அவதானிப்புகளையும் சேர்ப்பதன் மூலம் கணக்கிடப்படுகிறது, பின்னர் கீழே காட்டப்பட்டுள்ளபடி அவதானிப்புகளின் எண்ணிக்கையால் முடிவைப் பிரிக்கவும்.
சராசரி = (அ1 + அ2 +…. + அn) / n
எடுத்துக்காட்டுகள்
இந்த சராசரி ஃபார்முலா எக்செல் வார்ப்புருவை இங்கே பதிவிறக்கம் செய்யலாம் - சராசரி ஃபார்முலா எக்செல் வார்ப்புருஎடுத்துக்காட்டு # 1
சுற்றுச்சூழல் அறிவியலுக்கான பட்டமளிப்பு திட்டத்தில் சேர்ந்த ஜானின் உதாரணத்தை எடுத்துக் கொள்வோம். மூன்று ஆண்டு பட்டப்படிப்பு ஆறு செமஸ்டர்களாக பிரிக்கப்பட்டுள்ளது மற்றும் இறுதி சராசரி சதவீதம் அனைத்து செமஸ்டர்களிலும் அடித்த சதவீதங்களின் அடிப்படையில் கணக்கிடப்படுகிறது. ஜான் பின்வரும் மதிப்பெண்ணின் அடிப்படையில் இறுதி சதவீதத்தைக் கணக்கிடுங்கள்:
சராசரி சதவீதத்தைக் கணக்கிடுவதற்கான தரவு கீழே கொடுக்கப்பட்டுள்ளது.

கொடுக்கப்பட்ட,
a1 = 79%, அ2 = 81%, அ3 = 74%, அ4 = 70%, அ5 = 82%, அ6 = 85%, n = 6
மேற்கண்ட தகவல்களைப் பயன்படுத்தி, சராசரியின் கணக்கீடு பின்வருமாறு இருக்கும்,

- சராசரி = (79% + 81% + 74% + 70% + 82% + 85%) / 6
சராசரி இருக்கும் -

- சராசரி = 78.50%
எனவே, பட்டப்படிப்பு திட்டத்தில் டேவிட் 78.5% இறுதி சதவீதத்தைப் பெற்றார்.
பயன்கள்
“சராசரி” என்ற பெயர் குறிப்பிடுவது போல, இது ஒரு சில அவதானிப்புகளில் மத்திய புள்ளியைக் குறிக்கிறது, மேலும் இது கணிதத் துறையில் பயன்படுத்தப்படும்போது, அது பொதுவாக எண்களின் குழுவின் சராசரி எண்ணைக் குறிக்கிறது. ஒரு நபரின் அல்லது விஷயங்களின் பிரதிநிதித்துவமான எண்ணை வெளிப்படுத்த இந்த சொல் பெரும்பாலும் பயன்படுத்தப்படுகிறது. இது மிகவும் முக்கியமானது, ஏனெனில் இது ஒரு பெரிய எண்ணிக்கையிலான தரவை ஒரு மதிப்பாக சுருக்கமாகக் கூற உதவுகிறது, மேலும் அசல் தரவுகளுக்குள் ஒற்றை மதிப்பைச் சுற்றி சில முரண்பாடுகள் இருப்பதையும் இது குறிக்கிறது, இது மையப் போக்குக் கோட்பாட்டின் மிக முக்கியமான பகுதியாகும்.