பாண்ட் ஃபார்முலா | எடுத்துக்காட்டுகளுடன் படிப்படியாக பத்திர மதிப்பைக் கணக்கிடுதல்
பாண்ட் ஃபார்முலா என்றால் என்ன?
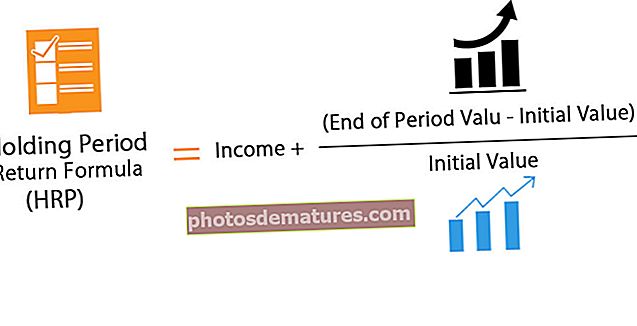
பாண்ட் ஃபார்முலா பரிசீலனையில் உள்ள பத்திரத்தின் நியாயமான மதிப்பைக் கணக்கிடுவதற்குப் பயன்படுத்தப்படும் சூத்திரத்தைக் குறிக்கிறது மற்றும் பத்திரத்தின் சூத்திர மதிப்பின் படி பொருத்தமான தள்ளுபடி வீதத்தால் தள்ளுபடி செய்யப்பட்ட பின்னர் பத்திரத்தின் அனைத்து கூப்பன் கொடுப்பனவுகளின் தற்போதைய மதிப்பைச் சேர்ப்பதன் மூலம் கணக்கிடப்படுகிறது. பத்திரங்களின் முக மதிப்பின் தற்போதைய மதிப்பு, பாண்டின் முக மதிப்பை 1 பிளஸ் தள்ளுபடி வீதம் அல்லது முதிர்ச்சிக்கான மகசூல் ஆகியவற்றின் மூலம் டைவ் செய்வதன் மூலம் கணக்கிடப்படுகிறது.

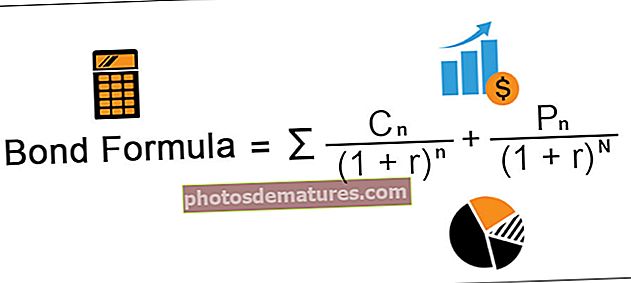
எங்கே,
- சிn பத்திரத்தின் கூப்பன் ஆகும்
- பிn பத்திரத்தின் முதன்மை
- n என்பது காலங்களின் எண்ணிக்கை
- N என்பது முதிர்வு காலம்
- r என்பது தள்ளுபடி வீதம் அல்லது முதிர்ச்சிக்கான மகசூல்
படிப்படியாக ஒரு பத்திரத்தின் கணக்கீடு
பத்திரத்தின் கணக்கீட்டை பின்வரும் படிகளில் புரிந்து கொள்ளலாம்:
- படி 1 - மாதாந்திர, ஆண்டு, காலாண்டு அல்லது அரை வருடாந்திர அதிர்வெண்ணைப் பொறுத்து கூப்பன் பணப்புழக்கங்களைக் கணக்கிடுங்கள்.
- படி 2 - முதிர்வு விகிதத்திற்கு பொருத்தமான மகசூல் மூலம் கூப்பனை தள்ளுபடி செய்யுங்கள்
- படி 3 - தள்ளுபடி செய்யப்பட்ட அனைத்து கூப்பன்களின் மொத்தத்தையும் எடுத்துக் கொள்ளுங்கள்
- படி 4 - இப்போது, முதிர்ச்சியில் செலுத்தப்படும் பத்திரத்தின் முக மதிப்பின் தள்ளுபடி மதிப்பைக் கணக்கிடுங்கள்.
- படி 5 - படி 3 மற்றும் படி 4 இல் வந்த மதிப்பைச் சேர்க்கவும், இது பத்திரத்தின் மதிப்பாக இருக்கும்.
எடுத்துக்காட்டுகள்
இந்த பாண்ட் ஃபார்முலா எக்செல் வார்ப்புருவை இங்கே பதிவிறக்கம் செய்யலாம் - பாண்ட் ஃபார்முலா எக்செல் வார்ப்புருஎடுத்துக்காட்டு # 1
6% வருடாந்திர கூப்பனை செலுத்தும் face 1,000 முக மதிப்பு பத்திரம் 8 ஆண்டுகளில் முதிர்ச்சியடையும் என்று வைத்துக் கொள்ளுங்கள். சந்தையில் முதிர்ச்சிக்கான தற்போதைய மகசூல் 6.5% ஆக உள்ளது. கொடுக்கப்பட்ட தகவலின் அடிப்படையில், நீங்கள் பத்திர மதிப்பைக் கணக்கிட வேண்டும்.
தீர்வு
- பத்திரத்தின் பணப்புழக்கங்கள் வருடாந்திர கூப்பன்கள் ஆகும், இது காலம் 8 வரை 1,000 x 6% மற்றும் 8 ஆம் காலகட்டத்தில், முதன்மை 1,000 திரும்பும்.
பத்திர மதிப்பைக் கணக்கிடுவதற்கு கீழே கொடுக்கப்பட்டுள்ள தரவைப் பயன்படுத்தவும்

ஆண்டு 1 க்கான பணப்புழக்கத்தின் கணக்கீடு

- =1000*6%
- =60.00
இதேபோல், மீதமுள்ள ஆண்டுகளுக்கான பணப்புழக்கங்களை நாம் கணக்கிடலாம்.

பத்திர மதிப்பின் கணக்கீடு பின்வருமாறு,

=60/(1+6.50%)^1+60/(1+6.50%)^2+60/(1+6.50%)^3+60/(1+6.50%)^4+60/(1+6.50%)^5+60/(1+6.50%)^6+60/(1+6.50%)^7+60/(1+6.50%)^8
பத்திர மதிப்பு இருக்கும் -

- பத்திர மதிப்பு = 969.56
எடுத்துக்காட்டு # 2
ஃபென்னி மே என்பது அமெரிக்க சந்தையில் பிரபலமான பத்திரங்களில் ஒன்றாகும். பத்திரங்களில் ஒன்று காலாண்டு வட்டி 3.5% மற்றும் பத்திரத்தின் முக மதிப்பு $ 1,000 ஆகும். பத்திரம் 5 ஆண்டுகளில் முதிர்ச்சியடையும். சந்தையில் நிலவும் முதிர்ச்சிக்கான தற்போதைய மகசூல் 5.32% ஆகும். மேலே உள்ள தகவல்களின் அடிப்படையில், பத்திர புள்ளிகளின் கணக்கீட்டை சதவீத புள்ளிகளில் செய்ய வேண்டும்.
தீர்வு
- பத்திரத்தின் பணப்புழக்கங்கள் காலாண்டு கூப்பன்கள் ஆகும், அவை 20 x (5 ஆண்டுகள் x 4) வரை 1,000 x 3.5% / 4 ஆகும், மேலும் 20 ஆம் காலகட்டத்தில், முதன்மை 1,000 திரும்பும்.
- இப்போது நாம் அவற்றை YTM இல் தள்ளுபடி செய்வோம், இது 5.32% / 4 ஆகும், இது 1.33% ஆக இருக்கும்.
பத்திர மதிப்பைக் கணக்கிடுவதற்கு கீழே கொடுக்கப்பட்டுள்ள தரவைப் பயன்படுத்தவும்

ஆண்டுக்கான பணப்புழக்கத்தின் கணக்கீடு

- =0.88%*1000
- =8.75
இதேபோல், மீதமுள்ள ஆண்டுகளுக்கான பணப்புழக்கங்களை நாம் கணக்கிடலாம்

ஆண்டு 1 க்கான தள்ளுபடி வீதம்

- =1/(1+1.33%)^1
- =0.986875
இதேபோல், மீதமுள்ள ஆண்டுகளுக்கான தள்ளுபடி விகிதத்தை நாம் கணக்கிடலாம்

ஆண்டுக்கான தள்ளுபடி செய்யப்பட்ட பணப்புழக்கங்களின் கணக்கீடு

- =8.75*0.986875
- =8.64
இதேபோல், மீதமுள்ள ஆண்டுகளுக்கு தள்ளுபடி செய்யப்பட்ட பணப்புழக்கங்களை நாம் கணக்கிடலாம்
தள்ளுபடி செய்யப்பட்ட பணப்புழக்கங்களின் கணக்கீடு

பத்திர மதிப்பு இருக்கும் -

- பத்திர மதிப்பு = 920.56
எனவே, பத்திரத்தின் மதிப்பு 920.56 / 1000 ஆக இருக்கும், இது 92.056% ஆகும்.
எடுத்துக்காட்டு # 3
3 ஆண்டுகளில் முதிர்ச்சியடையும் பத்திரங்களில் ஒன்று 0 1,019.78 க்கு வர்த்தகம் செய்யப்படுகிறது மற்றும் 6.78% அரை ஆண்டு கூப்பனை செலுத்துகிறது. சந்தையில் தற்போதைய மகசூல் 5.85% ஆகும். திரு. எக்ஸ் இந்த பத்திரத்தில் முதலீடு செய்ய விரும்புகிறார், அது குறைவாக மதிப்பிடப்படுகிறதா என்பதை அறிய விரும்புகிறீர்களா?
தீர்வு
- பத்திரத்தின் பணப்புழக்கங்கள் காலாண்டு கூப்பன்கள் ஆகும், அவை 6 x (3 ஆண்டுகள் x 2) வரை 1,000 x 6.78% / 2 மற்றும் 6 ஆம் காலகட்டத்தில், முதன்மை 1,000 திரும்பும்.
- இப்போது நாம் அவற்றை YTM இல் தள்ளுபடி செய்வோம், இது 5.85% / 2 ஆகும், இது 2.93% ஆக இருக்கும்
பத்திர மதிப்பைக் கணக்கிடுவதற்கு கீழே கொடுக்கப்பட்டுள்ள தரவைப் பயன்படுத்தவும்

ஆண்டிற்கான பணப்புழக்கத்தின் கணக்கீடு

இதேபோல், மீதமுள்ள ஆண்டுகளுக்கான பணப்புழக்கங்களை நாம் கணக்கிடலாம்.

பத்திர மதிப்பின் கணக்கீடு பின்வருமாறு,

=33.90/(1+2.93%)^1+33.90/(1+2.93%)^2+33.90/(1+2.93%)^3+33.90/(1+2.93%)^4+33.90/(1+2.93%)^5+33.90/(1+2.93%)^6
பத்திர மதிப்பு இருக்கும் -

- பத்திர மதிப்பு = 1025.25
சம்பந்தம் மற்றும் பயன்கள்
பத்திர விலை நிர்ணயம் அல்லது மதிப்பீடு முதலீட்டாளருக்கு முதலீடு செய்யப்பட வேண்டுமா இல்லையா என்பதை தீர்மானிக்க உதவும். இந்த பத்திர சூத்திரம் பத்திர வாழ்க்கையின் போது அனைத்து பணப்புழக்கங்களின் தற்போதைய மதிப்பைக் கண்டுபிடிக்கும். இது பொருத்தமான முதலீடா இல்லையா என்பதை தீர்மானிக்கவும் இது உதவும். இந்த பத்திர சமன்பாட்டின் மூலம் பத்திரத்தின் விலையை அவர்கள் பெறும்போது பத்திரத்தின் வருவாய் விகிதத்தையும் ஒருவர் காணலாம்.