காலாண்டு விலகல் (ஃபார்முலா) | எடுத்துக்காட்டுகளுடன் படி கணக்கீடு
காலாண்டு விலகல் என்றால் என்ன?
காலாண்டு விலகல் அதிர்வெண் விநியோகத்தில் முதல் காலாண்டுக்கும் மூன்றாவது காலாண்டுக்கும் இடையிலான வேறுபாட்டை அடிப்படையாகக் கொண்டது மற்றும் வேறுபாடு இடைநிலை வரம்பு என்றும் அழைக்கப்படுகிறது, இரண்டால் வகுக்கப்பட்டுள்ள வேறுபாடு காலாண்டு விலகல் அல்லது அரை இடைநிலை வரம்பு என அழைக்கப்படுகிறது.
ஒரு எளிய விநியோகம் அல்லது அதிர்வெண் விநியோகத்தின் 3 வது காலாண்டுக்கும் 1 வது காலாண்டுக்கும் இடையிலான வேறுபாடு அல்லது மாறுபாட்டின் பாதியை ஒருவர் எடுக்கும்போது, அது காலாண்டு விலகல் ஆகும்.
ஃபார்முலா
ஒரு குவார்டைல் விலகல் (Q.D.) சூத்திரம் புள்ளிவிவரங்களில் பரவலை அளவிட அல்லது வேறு வார்த்தைகளில் சொன்னால் சிதறலை அளவிட பயன்படுத்தப்படுகிறது. இதை அரை இடை-காலாண்டு வீச்சு என்றும் அழைக்கலாம்.
கே.டி. = Q3 - Q1 / 2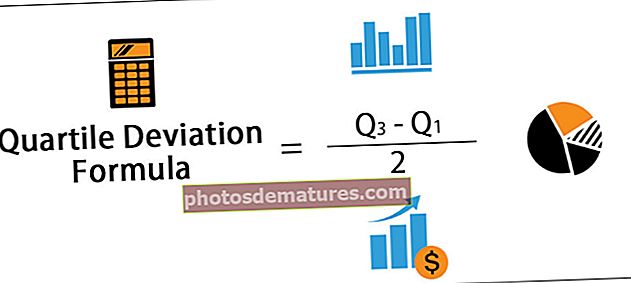
- சூத்திரத்தில் Q3 மற்றும் Q1 ஆகியவை கணக்கீட்டில் முதல் 25% மற்றும் முறையே 25% தரவைக் குறைக்கின்றன, மேலும் இந்த இரண்டிற்கும் இடையில் வேறுபாடு எடுக்கப்படும்போது, இந்த எண்ணிக்கை பாதியாக இருக்கும்போது அது பரவல் அல்லது சிதறல் நடவடிக்கைகளை அளிக்கிறது.
- எனவே, குவார்டைல் விலகலைக் கணக்கிட, நீங்கள் முதலில் Q1 ஐக் கண்டுபிடிக்க வேண்டும், பின்னர் இரண்டாவது படி Q3 ஐக் கண்டுபிடித்து, பின்னர் இரண்டின் வித்தியாசத்தையும் எடுத்துக் கொள்ளுங்கள், இறுதி படி 2 ஆல் வகுக்க வேண்டும்.
- திறந்த தரவுக்கான சிதறலின் சிறந்த முறைகளில் இதுவும் ஒன்றாகும்.
எடுத்துக்காட்டுகள்
இந்த குவார்டைல் விலகல் ஃபார்முலா எக்செல் வார்ப்புருவை இங்கே பதிவிறக்கம் செய்யலாம் - காலாண்டு விலகல் ஃபார்முலா எக்செல் வார்ப்புருஎடுத்துக்காட்டு # 1
பின்வரும் எண்களின் தரவு தொகுப்பைக் கவனியுங்கள்: 22, 12, 14, 7, 18, 16, 11, 15, 12. நீங்கள் காலாண்டு விலகலைக் கணக்கிட வேண்டும்.
தீர்வு:
முதலில், Q3 மற்றும் Q1 ஐக் கண்டுபிடிப்பதற்கும், நகல்களைத் தவிர்ப்பதற்கும் ஏறுவரிசையில் தரவை ஏற்பாடு செய்ய வேண்டும்.
7, 11, 12, 13, 14, 15, 16, 18, 22
Q1 இன் கணக்கீடு பின்வருமாறு செய்யப்படலாம்,
Q1 = ¼ (9 + 1)
=¼ (10)
Q1=2.5 கால
Q3 கணக்கீடு பின்வருமாறு செய்ய முடியும்,
Q3 = (9 + 1)
=¾ (10)
Q3= 7.5 கால
காலாண்டு விலகலைக் கணக்கிடுவது பின்வருமாறு செய்யப்படலாம்,
- Q1 என்பது 2 வது சராசரியாகும், இது 11 மற்றும் 3 வது மற்றும் 4 வது மற்றும் 0.5 க்கு இடையிலான வித்தியாசத்தின் விளைவை சேர்க்கிறது (இது 12-11) * 0.5 = 11.50.
- Q3 என்பது 7 வது கால மற்றும் 0.5 இன் தயாரிப்பு மற்றும் 8 மற்றும் 7 வது காலத்திற்கு இடையிலான வேறுபாடு (18-16) * 0.5 மற்றும் இதன் விளைவாக 16 + 1 = 17 ஆகும்.
கே.டி. = Q3 - Q1 / 2
காலாண்டு விலகல் சூத்திரத்தைப் பயன்படுத்தி, எங்களிடம் (17-11.50) / 2 உள்ளது
=5.5/2
கே.டி.=2.75.
எடுத்துக்காட்டு # 2
ஹாரி லிமிடெட். ஒரு ஜவுளி உற்பத்தியாளர் மற்றும் ஒரு வெகுமதி கட்டமைப்பில் வேலை செய்கிறார். ஒரு புதிய முயற்சியைத் தொடங்க நிர்வாகம் விவாதத்தில் உள்ளது, ஆனால் அவர்கள் முதலில் தங்கள் உற்பத்தி பரவல் எவ்வளவு என்பதை அறிய விரும்புகிறார்கள்.
(சராசரி) ஒரு ஊழியருக்கு கடந்த 10 நாட்களாக நிர்வாகம் அதன் சராசரி தினசரி உற்பத்தி தரவை சேகரித்துள்ளது.
155, 169, 188, 150, 177, 145, 140, 190, 175, 156.
நிர்வாகம் சிதறலைக் கண்டறிய உதவும் காலாண்டு விலகல் சூத்திரத்தைப் பயன்படுத்தவும்.
தீர்வு:
இங்கே அவதானிப்புகளின் எண்ணிக்கை 10 மற்றும் எங்கள் முதல் படி தரவு n ஏறும் வரிசையை ஏற்பாடு செய்வதாகும்.
140, 145, 150, 155, 156, 169, 175, 177, 188, 190
Q1 இன் கணக்கீடு பின்வருமாறு செய்யப்படலாம்,
Q1 = ¼ (n + 1) வது சொல்
=¼ (10+1)
=¼ (11)
Q1= 2.75 வது கால
Q3 கணக்கீடு பின்வருமாறு செய்ய முடியும்,
Q3 = ¾ (n + 1) வது சொல்
=¾ (11)
Q3= 8.25 கால
காலாண்டு விலகலைக் கணக்கிடுவது பின்வருமாறு செய்யப்படலாம்,
- 2 வது தவணை 145 மற்றும் இப்போது இந்த 0.75 * (150 - 145) இல் 3.75 ஆக சேர்க்கப்பட்டுள்ளது, இதன் விளைவாக 148.75 ஆகும்
- 8 வது தவணை 177 மற்றும் இப்போது இந்த 0.25 * (188 - 177) இல் 2.75 ஆகவும், இதன் விளைவாக 179.75 ஆகவும் சேர்க்கப்படுகிறது
கே.டி. = Q3 - Q1 / 2
காலாண்டு விலகல் சூத்திரத்தைப் பயன்படுத்தி, எங்களிடம் (179.75-148.75) / 2 உள்ளது
=31/2
கே.டி.=15.50.
எடுத்துக்காட்டு # 3
ரியானின் சர்வதேச அகாடமி தங்கள் மாணவர்களின் சதவீத மதிப்பெண்கள் எவ்வளவு பரவுகின்றன என்பதை பகுப்பாய்வு செய்ய விரும்புகிறது.
தரவு 25 மாணவர்களுக்கானது.

% மதிப்பெண்களில் சிதறலைக் கண்டறிய குவார்டைல் விலகல் சூத்திரத்தைப் பயன்படுத்தவும்.
தீர்வு:
இங்கே அவதானிப்புகளின் எண்ணிக்கை 25 ஆகும், எங்கள் முதல் படி தரவை ஏறுவரிசையில் ஏற்பாடு செய்யும்.

Q1 இன் கணக்கீடு பின்வருமாறு செய்யப்படலாம்,
Q1 = ¼ (n + 1) வது சொல்
=¼ (25+1)
=¼ (26)
Q1= 6.5 வது கால
Q3 கணக்கீடு பின்வருமாறு செய்ய முடியும்,
Q3 = ¾ (n + 1) வது சொல்
=¾ (26)
Q3 = 19.50 கால
காலாண்டு விலகல் அல்லது அரை இடைவெளியின் வரம்பைக் கணக்கிடுவது பின்வருமாறு செய்யப்படலாம்,
- 6 வது கால அளவு 154 ஆகும், இப்போது இந்த 0.50 * (156 - 154) இல் 1 ஐ சேர்க்கிறது, இதன் விளைவாக 155.00 ஆகும்
- 19 வது காலப்பகுதி 177 ஆகும், இப்போது இந்த 0.50 * (177 - 177) உடன் சேர்க்கிறது, இது 0 மற்றும் இதன் விளைவாக 177 ஆகும்
கே.டி. = Q3 - Q1 / 2
காலாண்டு விலகல் சூத்திரத்தைப் பயன்படுத்தி, எங்களிடம் (177-155) / 2 உள்ளது
=22/2
கே.டி.= 11.
எடுத்துக்காட்டு # 4
நடைமுறை எடுத்துக்காட்டு I க்கான எக்செல் வார்ப்புரு மூலம் மதிப்பை இப்போது தீர்மானிப்போம்.
தீர்வு:
காலாண்டு விலகலைக் கணக்கிடுவதற்கு பின்வரும் தரவைப் பயன்படுத்தவும்.

Q1 இன் கணக்கீடு பின்வருமாறு செய்யப்படலாம்,

Q1=148.75
Q3 கணக்கீடு பின்வருமாறு செய்ய முடியும்,

Q3= 179.75
காலாண்டு விலகலைக் கணக்கிடுவது பின்வருமாறு செய்யப்படலாம்,

காலாண்டு விலகல் சூத்திரத்தைப் பயன்படுத்தி, எங்களிடம் (179.75-148.75) / 2 உள்ளது
கே.டி. இருக்கும் -

QD = 15.50
சம்பந்தம் மற்றும் பயன்கள்
காலாண்டு விலகல் இது அரை இடைநிலை வரம்பாகவும் புகழ்பெற்றது. மீண்டும், 3 வது மற்றும் 1 வது காலாண்டுகளுக்கு இடையிலான மாறுபாட்டின் வேறுபாடு இடைநிலை வரம்பு என அழைக்கப்படுகிறது. கொடுக்கப்பட்ட தரவுத்தொகுப்பின் அவதானிப்புகள் அல்லது மதிப்புகள் சராசரி அல்லது அவற்றின் சராசரியிலிருந்து எந்த அளவிற்கு பரவுகின்றன என்பதை இடைநிலை வரம்பு சித்தரிக்கிறது. குவார்டைல் விலகல் அல்லது அரை இடைநிலை வரம்பு என்பது ஒரு சந்தர்ப்பத்தில் பயன்படுத்தப்படும் பெரும்பான்மையாகும், இது அவதானிப்புகள் சிதறடிக்கப்படுவது அல்லது கொடுக்கப்பட்ட தொடரின் பிரதான அல்லது நடுத்தர உடலில் இருக்கும் கொடுக்கப்பட்ட தரவுத் தொகுப்புகளின் மாதிரிகள் பற்றி ஒரு ஆய்வைக் கற்றுக்கொள்ள அல்லது சொல்ல விரும்பினால். இந்த வழக்கு வழக்கமாக தரவு அல்லது அவதானிப்புகள் கொடுக்கப்பட்ட தரவுகளின் தொகுப்பு அல்லது தொடரின் பிரதான உடலில் அல்லது நடுவில் தீவிரமாக பொய் சொல்லும் ஒரு விநியோகத்தில் நிகழும் மற்றும் விநியோகம் அல்லது மதிப்புகள் உச்சத்தை நோக்கி பொய் சொல்லாது, அவை பொய் என்றால் அவை கணக்கீட்டிற்கு அதிக முக்கியத்துவம் இல்லை.