புள்ளிவிவரங்களில் இசட் டெஸ்ட் ஃபார்முலா | படிப்படியான கணக்கீடு (எடுத்துக்காட்டுகள்)
புள்ளிவிவரத்தில் இசட் சோதனையை கணக்கிடுவதற்கான சூத்திரம்
புள்ளிவிவரங்களில் இசட் டெஸ்ட் என்பது கருதுகோள் சோதனையை குறிக்கிறது, இது இரண்டு மாதிரிகள் கணக்கிடப்பட்டவை வேறுபட்டதா என்பதை தீர்மானிக்க பயன்படுகிறது, நிலையான விலகல்கள் கிடைத்தால் மற்றும் மாதிரி பெரியதாக இருந்தால்.
Z = (x - μ) / ø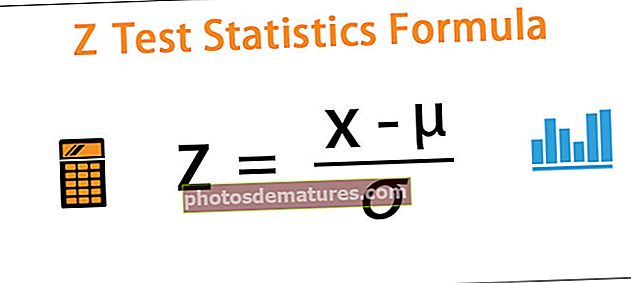
x = மக்கள்தொகையில் இருந்து எந்த மதிப்பும்
- μ = மக்கள் தொகை சராசரி
- Population = மக்கள் தொகை நியமச்சாய்வு
ஒரு மாதிரியின் விஷயத்தில், x- மதிப்பிலிருந்து மாதிரி சராசரியைக் கழிப்பதன் மூலம் மதிப்பின் z- சோதனை புள்ளிவிவரங்களுக்கான சூத்திரம் கணக்கிடப்படுகிறது, பின்னர் இதன் விளைவாக மாதிரி நிலையான விலகலால் வகுக்கப்படுகிறது. கணித ரீதியாக, இது,
Z = (x - x_mean) / கள்எங்கே
- x = மாதிரியிலிருந்து எந்த மதிப்பும்
- x_mean = மாதிரி சராசரி
- s = மாதிரி நிலையான விலகல்
இசட் டெஸ்ட் கணக்கீடு (படிப்படியாக)
ஒரு மக்கள்தொகைக்கான z- சோதனை புள்ளிவிவரங்களுக்கான சூத்திரம் பின்வரும் படிகளைப் பயன்படுத்துவதன் மூலம் பெறப்படுகிறது:
- படி 1: முதலாவதாக, மக்கள்தொகையில் கைப்பற்றப்பட்ட அவதானிப்பின் அடிப்படையில் மக்கள்தொகை வழிமுறைகளையும் மக்கள்தொகை நிலையான விலகலையும் கணக்கிடுங்கள், மேலும் ஒவ்வொரு அவதானிப்பும் x ஆல் குறிக்கப்படுகிறதுநான். மக்கள்தொகையில் மொத்த அவதானிப்புகளின் எண்ணிக்கை என்.
மக்கள் தொகை என்றால்,

மக்கள்தொகை நிலையான விலகல்,

- படி 2: இறுதியாக, z- சோதனை புள்ளிவிவரங்கள் மாறிலிருந்து மக்கள்தொகை சராசரியைக் கழிப்பதன் மூலம் கணக்கிடப்படுகின்றன, பின்னர் இதன் விளைவாக கீழே காட்டப்பட்டுள்ளபடி மக்கள் தொகை நியமச்சாய்வு மூலம் வகுக்கப்படுகிறது.
Z = (x - μ) / ø
ஒரு மாதிரிக்கான z- சோதனை புள்ளிவிவரங்களுக்கான சூத்திரம் பின்வரும் படிகளைப் பயன்படுத்தி பெறப்படுகிறது:
- படி 1: முதலாவதாக, மாதிரி சராசரி மற்றும் மாதிரி நிலையான விலகலை மேலே உள்ளதைப் போலவே கணக்கிடுங்கள். இங்கே, மாதிரியில் உள்ள மொத்த அவதானிப்புகளின் எண்ணிக்கை n ஆல் குறிக்கப்படுகிறது, அதாவது n <N.
மாதிரி சராசரி,

மாதிரி நிலையான விலகல்,

- படி 2: இறுதியாக, z- சோதனை புள்ளிவிவரங்கள் x- மதிப்பிலிருந்து மாதிரி சராசரியைக் கழிப்பதன் மூலம் கணக்கிடப்படுகின்றன, பின்னர் இதன் விளைவாக கீழே காட்டப்பட்டுள்ளபடி மாதிரி நிலையான விலகலால் வகுக்கப்படுகிறது.
Z = (x - x_mean) / கள்
எடுத்துக்காட்டுகள்
இந்த இசட் டெஸ்ட் ஃபார்முலா எக்செல் வார்ப்புருவை இங்கே பதிவிறக்கம் செய்யலாம் - இசட் டெஸ்ட் ஃபார்முலா எக்செல் வார்ப்புருஎடுத்துக்காட்டு # 1
வகுப்புத் தேர்வுக்குத் தோன்றிய ஒரு பள்ளியில் உள்ள மாணவர்களின் எண்ணிக்கையை நாம் கருதுவோம். சோதனையில் சராசரி மதிப்பெண் 75 மற்றும் நிலையான விலகல் 15. சோதனையில் 90 மதிப்பெண்கள் பெற்ற டேவிட் இசட்-டெஸ்ட் மதிப்பெண்ணைத் தீர்மானிக்கவும்.
கொடுக்கப்பட்ட,
- மக்கள் தொகை, μ = 75
- மக்கள்தொகை நிலையான விலகல், ơ = 15

எனவே, z- சோதனை புள்ளிவிவரங்களை இவ்வாறு கணக்கிடலாம்,

Z = (90 - 75) / 15
Z சோதனை புள்ளிவிவரங்கள் இருக்கும் -

- Z = 1
ஆகையால், டேவிட் சோதனை மதிப்பெண் என்பது மக்கள்தொகையின் சராசரி மதிப்பெண்ணை விட ஒரு நிலையான விலகலாகும், அதாவது z- மதிப்பெண் அட்டவணையின்படி, 84.13% மாணவர்கள் டேவிட்டை விட குறைந்த மதிப்பெண் பெற்றவர்கள்.
எடுத்துக்காட்டு # 2
ஒரு வாரத்தில் எத்தனை பென்சில்கள் பயன்படுத்தப்படுகின்றன என்பதைக் கணக்கெடுப்பதற்காக மாதிரி குழுவின் ஒரு பகுதியாக தேர்ந்தெடுக்கப்பட்ட 30 மாணவர்களின் உதாரணத்தை எடுத்துக்கொள்வோம். கொடுக்கப்பட்ட பதில்களின் அடிப்படையில் 3 வது மாணவருக்கான z- சோதனை மதிப்பெண்ணை தீர்மானிக்கவும்: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 , 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7.
கொடுக்கப்பட்ட,
- x = 5, 3 வது மாணவரின் பதில் 5 என்பதால்
- மாதிரி அளவு, n = 30
மாதிரி சராசரி, = (3 + 2 + 5 + 6 + 4 + 7 + 4 + 3 + 3 + 8 + 3 + 1 + 3 + 6 + 5 + 2 + 4 + 3 + 6 + 4 + 5 + 2 + 2 + 4 + 4 + 2 + 8 + 3 + 6 + 7) / 30
சராசரி = 4.17
இப்போது, மேலே உள்ள சூத்திரத்தைப் பயன்படுத்தி மாதிரி நிலையான விலகலைக் கணக்கிட முடியும்.
= 1.90
எனவே, 3 வது மாணவருக்கான z- சோதனை மதிப்பெண்,
Z = (x - x) / s
- Z = (5 –17) / 1.90
- இசட் = 0.44
ஆகையால், 3 வது மாணவரின் பயன்பாடு மாதிரியின் சராசரி பயன்பாட்டிற்கு மேல் 0.44 மடங்கு ஆகும், அதாவது z- மதிப்பெண் அட்டவணையின்படி, 67% மாணவர்கள் 3 வது மாணவரை விட குறைவான பென்சில்களைப் பயன்படுத்துகின்றனர்.
எடுத்துக்காட்டு # 3
ஒரு வாரத்தில் எத்தனை பென்சில்கள் பயன்படுத்தப்படுகின்றன என்பதைக் கணக்கெடுப்பதற்காக மாதிரி குழுவின் ஒரு பகுதியாக தேர்ந்தெடுக்கப்பட்ட 30 மாணவர்களின் உதாரணத்தை எடுத்துக்கொள்வோம். கொடுக்கப்பட்ட பதில்களின் அடிப்படையில் 3 வது மாணவருக்கான z- சோதனை மதிப்பெண்ணை தீர்மானிக்கவும்: 3, 2, 5, 6, 4, 7, 4, 3, 3, 8, 3, 1, 3, 6, 5, 2, 4 , 3, 6, 4, 5, 2, 2, 4, 4, 2, 8, 3, 6, 7.
இசட் டெஸ்ட் புள்ளிவிவரங்களை கணக்கிடுவதற்கான தரவு கீழே கொடுக்கப்பட்டுள்ளது


இசட் டெஸ்ட் புள்ளிவிவரங்களின் விரிவான கணக்கீட்டிற்கு கீழே கொடுக்கப்பட்டுள்ள எக்செல் தாளை நீங்கள் பார்க்கலாம்.
சம்பந்தம் மற்றும் பயன்கள்
Z- சோதனை புள்ளிவிவரங்களின் கருத்தைப் புரிந்துகொள்வது மிகவும் முக்கியம், ஏனென்றால் இது ஒரு சோதனை புள்ளிவிவரம் சம்பந்தப்பட்ட பூஜ்ய கருதுகோளின் கீழ் ஒரு சாதாரண விநியோகத்தைப் பின்பற்றுகிறதா இல்லையா என்பது விவாதத்திற்குரிய போதெல்லாம் பயன்படுத்தப்படுகிறது. இருப்பினும், மாதிரி அளவு 30 ஐ விட அதிகமாக இருக்கும்போது மட்டுமே ஒரு z- சோதனை பயன்படுத்தப்படுகிறது என்பதை நினைவில் கொள்ள வேண்டும், இல்லையெனில், t- சோதனை பயன்படுத்தப்படுகிறது.