photosdematures.com

EWMA இன் வரையறை (அதிவேகமாக எடை கொண்ட நகரும் சராசரி)

அதிவேகமாக எடையுள்ள நகரும் சராசரி (EWMA) என்பது வெவ்வேறு காரணிகளைக் கருத்தில் கொண்டு முடிவுகளையும் வெளியீட்டையும் சரிபார்த்து, எடைகளைக் கொடுத்து, செயல்திறனை மதிப்பிடுவதற்கும் முடிவுகளைக் கண்காணிப்பதன் மூலமும் போர்ட்ஃபோலியோவின் இயக்கத்தைக் கண்காணிக்கப் பயன்படும் தரவின் சராசரியைக் குறிக்கிறது. மேம்பாடுகளைச் செய்யுங்கள்

ஒரு EWMA க்கான எடை கடந்த காலங்களில் மேலும் செல்லும் ஒவ்வொரு காலகட்டத்திற்கும் அதிவேக வழியைக் குறைக்கிறது. மேலும், ஈ.டபிள்யூ.எம்.ஏ முன்பு கணக்கிடப்பட்ட சராசரியைக் கொண்டிருப்பதால், அதிவேகமாக எடையுள்ள நகரும் சராசரியின் விளைவாக ஒட்டுமொத்தமாக இருக்கும். இதன் காரணமாக, அனைத்து தரவு புள்ளிகளும் முடிவுக்கு பங்களிக்கும், ஆனால் அடுத்த காலகட்டம் EWMA கணக்கிடப்படுவதால் பங்களிப்பு காரணி குறையும்.

விளக்கம்

இந்த EWMA ஃபார்முலா ஒரு நேரத்தில் நகரும் சராசரியின் மதிப்பைக் காட்டுகிறது.

EWMA (t) = a * x (t) + (1-a) * EWMA (t-1)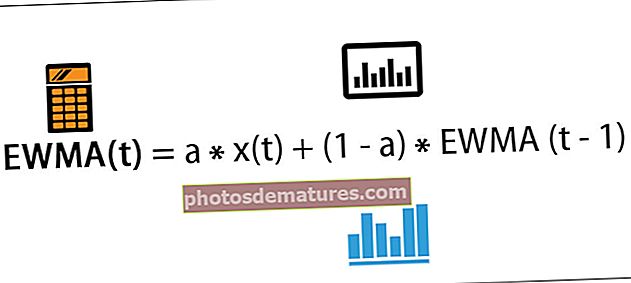

எங்கே

• EWMA (t) = நகரும் சராசரி t
• a = 0 மற்றும் 1 க்கு இடையில் அளவுரு மதிப்பைக் கலத்தல்
• x (t) = சமிக்ஞை x இன் மதிப்பு t

இந்த சூத்திரம் t நேரத்தில் நகரும் சராசரியின் மதிப்பைக் கூறுகிறது. பழைய தரவு கணக்கீடுக்கு வரும் விகிதத்தைக் காட்டும் ஒரு அளவுரு இங்கே. A இன் மதிப்பு 0 முதல் 1 வரை இருக்கும்.

ஒரு = 1 என்றால், EWMA ஐ அளவிட மிக சமீபத்திய தரவு மட்டுமே பயன்படுத்தப்பட்டுள்ளது. ஒரு 0 ஐ நெருங்கினால், பழைய தரவுகளுக்கு அதிக வெயிட்டேஜ் வழங்கப்படுகிறது, மேலும் 1 க்கு அருகில் இருந்தால் புதிய தரவுக்கு அதிக வெயிட்டேஜ் வழங்கப்பட்டுள்ளது.

EWMA இன் எடுத்துக்காட்டுகள்

அதிவேகமாக எடையுள்ள நகரும் சராசரிக்கான எடுத்துக்காட்டுகள் கீழே

இந்த EWMA எக்செல் வார்ப்புருவை இங்கே பதிவிறக்கம் செய்யலாம் - EWMA எக்செல் வார்ப்புரு

எடுத்துக்காட்டு # 1

கீழே உள்ள அட்டவணையின்படி 5 தரவு புள்ளிகளைக் கருத்தில் கொள்வோம்:

மற்றும் அளவுரு a = 30% அல்லது 0.3

எனவே EWMA (1) = 40

நேரம் 2 க்கான EWMA பின்வருமாறு

• EWMA (2) = 0.3 * 45 + (1-0.3) * 40.00
• = 41.5

இதேபோல் கொடுக்கப்பட்ட நேரங்களுக்கு அதிவேகமாக எடையுள்ள நகரும் சராசரியைக் கணக்கிடுங்கள் -

• EWMA (3) = 0.3 * 43 + (1-0.3) * 41.5 = 41.95
• EWMA (4) = 0.3 * 31 + (1-0.3) * 41.95 = 38.67
• EWMA (5) = 0.3 * 20 + (1-0.3) * 38.67 = 33.07

எடுத்துக்காட்டு # 2

ஒரு நகரத்தின் வெப்பநிலை ஞாயிற்றுக்கிழமை முதல் சனிக்கிழமை வரை டிகிரி செல்சியஸில் உள்ளது. ஒரு = 10% ஐப் பயன்படுத்தி வாரத்தின் ஒவ்வொரு நாளும் வெப்பநிலையின் நகரும் சராசரியைக் காண்போம்.

பயன்படுத்துகிறது a = 10% கீழேயுள்ள அட்டவணையில் ஒவ்வொரு நாளும் அதிவேகமாக எடையுள்ள நகரும் சராசரியைக் காண்போம்:

உண்மையான வெப்பநிலைக்கும் EWMA க்கும் இடையிலான ஒப்பீட்டைக் காட்டும் வரைபடம் கீழே உள்ளது:

= 10% ஐப் பயன்படுத்தி மென்மையானது மிகவும் வலுவானது என்பதை நாம் காண முடியும். பல வகையான நேரத் தொடர்கள் அல்லது தொடர்ச்சியான தரவுத்தொகுப்புகளுக்கான அதிவேக எடையுள்ள நகரும் சராசரியை நாம் தீர்க்க முடியும்.

நன்மைகள்

• தரவு அல்லது வெளியீட்டின் முழு வரலாற்றையும் பயன்படுத்தி சராசரியைக் கண்டறிய இது பயன்படுத்தப்படலாம். மற்ற எல்லா விளக்கப்படங்களும் ஒவ்வொரு தரவையும் தனித்தனியாக நடத்த முனைகின்றன.
• பயனர் தனது வசதிக்கு ஏற்ப ஒவ்வொரு தரவு புள்ளிகளுக்கும் வெயிட்டேஜ் கொடுக்க முடியும். பல்வேறு சராசரிகளை ஒப்பிட்டுப் பார்க்க இந்த வெயிட்டேஜை மாற்றலாம்.
• EWMA தரவை வடிவியல் ரீதியாகக் காட்டுகிறது. அந்த தரவு காரணமாக வெளிநாட்டவர்கள் நிகழும்போது அதிகம் பாதிக்கப்படாது.
• அதிவேகமாக எடையுள்ள நகரும் சராசரியின் ஒவ்வொரு தரவு புள்ளியும் நகரும் சராசரியின் புள்ளிகளைக் குறிக்கிறது.

வரம்புகள்

• குறிப்பிட்ட கால இடைவெளியில் தொடர்ச்சியான தரவு கிடைக்கும்போது மட்டுமே இதைப் பயன்படுத்த முடியும்.
• செயல்பாட்டில் ஒரு சிறிய மாற்றத்தை நாம் கண்டறிய விரும்பினால் மட்டுமே இதைப் பயன்படுத்த முடியும்.
• சராசரியைக் கணக்கிட இந்த முறையைப் பயன்படுத்தலாம். கண்காணிப்பு மாறுபாட்டிற்கு பயனர் வேறு சில நுட்பங்களைப் பயன்படுத்த வேண்டும்.

முக்கிய புள்ளிகள்

• அதிவேகமாக எடையுள்ள நகரும் சராசரியைப் பெற விரும்பும் தரவு நேரம் ஆர்டர் செய்யப்பட வேண்டும்.
• சத்தமாக நேர வரிசை தரவு புள்ளிகளில் சத்தத்தை குறைக்க இது மிகவும் உதவியாக இருக்கும், அவை மென்மையானவை என்று அழைக்கப்படுகின்றன.
• ஒவ்வொரு வெளியீட்டிற்கும் ஒரு வெயிட்டேஜ் வழங்கப்படுகிறது. மிக சமீபத்திய தரவு என்னவென்றால், அது பெறும் அதிக வெயிட்டேஜ்.
• சிறிய மாற்றத்தைக் கண்டறிவதில் இது மிகவும் நல்லது, ஆனால் பெரிய மாற்றத்தைக் கண்டறிவதில் மெதுவாக உள்ளது.
• துணைக்குழு மாதிரி அளவு 1 ஐ விட அதிகமாக இருக்கும்போது இதைப் பயன்படுத்தலாம்.
• நிஜ உலகில், இந்த முறையை வேதியியல் செயல்முறைகள் மற்றும் அன்றாட கணக்கியல் செயல்முறைகளில் பயன்படுத்தலாம்.
• வலைத்தள பார்வையாளர்கள் வார நாட்களில் ஏற்ற இறக்கங்களைக் காண்பிப்பதிலும் இதைப் பயன்படுத்தலாம்.

முடிவுரை

EWMA என்பது நேரத்திற்குட்பட்ட செயல்முறையின் சராசரியில் சிறிய மாற்றங்களைக் கண்டறியும் ஒரு கருவியாகும். அதிவேகமாக எடையுள்ள நகரும் சராசரியும் மிகவும் ஆய்வு செய்யப்பட்டு, நகரும் சராசரியைக் கண்டறிய ஒரு மாதிரியைப் பயன்படுத்துகிறது. கடந்த கால தரவுகளின் நிகழ்வு அடிப்படையை முன்னறிவிப்பதில் இது மிகவும் பயனுள்ளதாக இருக்கும். அதிவேகமாக எடையுள்ள நகரும் சராசரி என்பது அவதானிப்புகள் பொதுவாக விநியோகிக்கப்படுகின்றன என்று கருதப்படும் அடிப்படையாகும். அவற்றின் வெயிட்டேஜின் அடிப்படையில் கடந்த கால தரவுகளை இது பரிசீலித்து வருகிறது. கடந்த காலங்களில் தரவு அதிகமாக இருப்பதால், கணக்கீட்டிற்கான அதன் எடை அதிவேகமாகக் குறையும்.

EWMA அடிப்படையிலான வெவ்வேறு வெயிட்டேஜின் வேறுபட்ட தொகுப்பைக் கண்டறிய பயனர்கள் கடந்த கால தரவுகளுக்கு எடையைக் கொடுக்கலாம். வடிவியல் ரீதியாகக் காட்டப்படும் தரவுகளின் காரணமாக, வெளிநாட்டவர்கள் காரணமாக தரவு அதிகம் பாதிக்கப்படாது, எனவே இந்த முறையைப் பயன்படுத்தி அதிக மென்மையான தரவை அடைய முடியும்.