பாண்ட் சமமான மகசூல் ஃபார்முலா | படி கணக்கீடு (எடுத்துக்காட்டுகளுடன்)
பாண்ட் சமமான விளைச்சலைக் கணக்கிடுவதற்கான சூத்திரம் (BEY)
பத்திரங்களின் பெயரளவு அல்லது முக மதிப்பு மற்றும் அதன் கொள்முதல் விலை ஆகியவற்றுக்கு இடையிலான வேறுபாட்டைக் கண்டறிவதன் மூலம் பத்திர சமமான விளைச்சலைக் கணக்கிடுவதற்கு இந்த சூத்திரம் பயன்படுத்தப்படுகிறது, மேலும் இந்த முடிவுகளை அதன் விலையால் வகுக்க வேண்டும், மேலும் இந்த முடிவுகளை மேலும் 365 ஆல் பெருக்கி பின்னர் வகுக்க வேண்டும் முதிர்வு தேதி வரை மீதமுள்ள நாட்கள்.
ஒரு முதலீட்டாளர் பத்திர சமமான மகசூல் சூத்திரத்தை அறிந்து கொள்ள வேண்டும். இது முதலீட்டாளருக்கு ஒரு பத்திரத்தின் வருடாந்திர மகசூலைக் கணக்கிட அனுமதிக்கிறது, இது தள்ளுபடியில் விற்கப்படுகிறது.
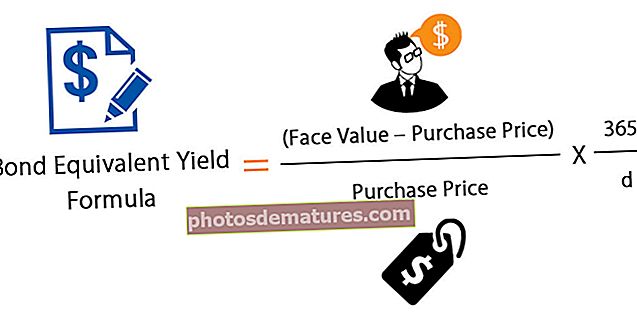
இங்கே, முதிர்ச்சிக்கு d = நாட்கள்
உதாரணமாக
இந்த பாண்ட் சமமான மகசூல் எக்செல் வார்ப்புருவை இங்கே பதிவிறக்கம் செய்யலாம் - பாண்ட் சமமான மகசூல் எக்செல் வார்ப்புரு
திரு. யாம்ஸி முதலீடுகளுக்காக பரிசீலிக்கும் இரண்டு பத்திரங்களைப் பற்றி குழப்பமடைகிறார். ஒரு பத்திரம் கொள்முதல் விலையாக ஒரு பத்திரத்திற்கு $ 100 மற்றும் மற்றொரு பத்திரத்திற்கு $ 90 வழங்குகிறது. நிலையான வருமான பத்திரங்கள் இரண்டிற்கும், அவர்கள் 6 மாதங்களுக்குப் பிறகு (முதல்) மற்றும் 12 மாதங்களுக்குப் பிறகு (இரண்டாவது) ஒரு பத்திரத்திற்கு 110 டாலர் வழங்குவார்கள். எந்த ஒரு திரு. யாம்சி முதலீடு செய்ய வேண்டும்?
இது இரண்டு நிலையான வருமான பத்திரங்களுக்கு இடையில் குழப்பமடைவதற்கான ஒரு சிறந்த வழக்கு.
எவ்வாறாயினும், திரு. யாம்சிக்கு எந்த முதலீடு அதிக பலன் தருகிறது என்பதைக் காண BEY ஐ எளிதாகக் கண்டுபிடிக்கலாம்.
முதல் பிணைப்புக்கு, இங்கே கணக்கீடு உள்ளது -
பத்திர சமமான மகசூல் = (முக மதிப்பு - கொள்முதல் விலை) / கொள்முதல் விலை * 365 / டி
- அல்லது, BEY = ($ 110 - $ 100) / $ 100 * 365/180
- அல்லது, BEY = $ 10 / $ 100 * 2.03
- அல்லது, BEY = 0.10 * 2.03 = 20.3%.
இப்போது, இரண்டாவது பிணைப்பிற்கான BEY ஐக் கணக்கிடுவோம்.
BEY = (முக மதிப்பு - கொள்முதல் விலை) / கொள்முதல் விலை * 365 / d
- அல்லது, BEY = ($ 110 - $ 90) / $ 90 * 365/365
- அல்லது, BEY = $ 20 / $ 90 * 1 = 22.22%.
இந்த இரண்டு பத்திரங்களுக்கும் BEY ஐக் கணக்கிடுவதன் மூலம், திரு. யாம்ஸி இரண்டாவது பத்திரத்தில் முதலீடு செய்ய வேண்டும் என்று நாம் எளிதாகக் கூறலாம்.
இருப்பினும், நேரம் ஒரு காரணியாகிவிட்டால், திரு. யாம்ஸி முதல் பத்திரத்தை தேர்வு செய்யலாம், ஏனெனில் 6 மாதங்கள் இது 20.3% வருமானத்தை அளிக்கிறது.
விளக்கம்
நீங்கள் உற்று நோக்கினால், பத்திர சமமான மகசூலுக்கு இந்த சூத்திரத்தின் இரண்டு பகுதிகள் இருப்பதை நீங்கள் காண்பீர்கள்.
- முதல் பகுதி முக மதிப்பு, கொள்முதல் விலை பற்றி பேசுகிறது. சுருக்கமாக, முதல் பகுதி முதலீட்டாளருக்கான முதலீட்டின் வருவாயை சித்தரிக்கிறது. எடுத்துக்காட்டாக, ஒரு முதலீட்டாளர் பத்திரத்திற்கான கொள்முதல் விலையாக $ 90 செலுத்தினால். 12 மாதங்களுக்குள் முதிர்ச்சியடையும் போது, அவர் $ 100 பெறுவார்; முதலீடுகளின் வருமானம் = ($ 100 - $ 90) / $ 90 = $ 10 / $ 90 = 11.11% ஆக இருக்கும்.
- இரண்டாவது பகுதி எல்லை எல்லை பற்றியது. பத்திரத்திற்கான முதிர்வு இப்போது 6 மாதங்கள் என்றால்; d 180 நாட்கள் இருக்கும். இரண்டாவது பகுதி இதன் விளைவாக - 365/180 = 2.03.
பயன்பாடு மற்றும் பொருத்தம்
ஒரு முதலீட்டாளராக, உங்களுக்கு பல விருப்பங்கள் உள்ளன. உங்களிடம் பல விருப்பங்கள் இருக்கும்போது, நீங்கள் அதிக வருமானத்தை வழங்கும் விருப்பத்தை மட்டுமே தேர்வு செய்வீர்கள்.
அதனால்தான் ஒரு குறிப்பிட்ட முதலீடு மற்ற முதலீடுகளை விட சிறந்ததா அல்லது மோசமானதா என்பதைக் கண்டறிய நீங்கள் பத்திர சமமான மகசூல் சூத்திரத்தைப் பயன்படுத்த வேண்டும்.
இருப்பினும், பத்திரத்திற்கு சமமான மகசூலைக் கணக்கிடுவதற்கு, இந்த முதலீடுகள் வருடாந்திர கொடுப்பனவுகளை வழங்காது என்பதை நினைவில் கொள்ள வேண்டும். நிலையான வருமான பத்திரங்களுக்கு இந்த சூத்திரத்தைப் பயன்படுத்தலாம். எடுத்துக்காட்டாக, ஒரு பத்திரத்தைப் பற்றி நீங்கள் கண்டறிந்தால், அது கொள்முதல் விலையில் தள்ளுபடியை அளிக்கிறது என்றால், முதலில் பத்திரத்திற்கு சமமான மகசூலைக் கண்டுபிடித்து, பின்னர் மேலே செல்லுங்கள் (நீங்கள் விரும்பினால்).
பாண்ட் சமமான மகசூல் கால்குலேட்டர்
நீங்கள் பின்வரும் பாண்ட் சமமான மகசூல் கால்குலேட்டரைப் பயன்படுத்தலாம்
| முக மதிப்பு | |
| கொள்முதல் விலை | |
| d | |
| பாண்ட் சமமான மகசூல் ஃபார்முலா = | |
| பாண்ட் சமமான மகசூல் ஃபார்முலா = |
| ||||||||||||
|
எக்செல் இல் பாண்ட் சமமான மகசூல் (எக்செல் வார்ப்புருவுடன்)
மேலே உள்ள அதே உதாரணத்தை இப்போது எக்செல் செய்வோம். இது மிகவும் எளிது. இந்த இரண்டு பிணைப்புகளுக்கும் நீங்கள் BEY ஐ கணக்கிட வேண்டும்.
வழங்கப்பட்ட வார்ப்புருவில் BEY ஐ எளிதாகக் கணக்கிடலாம்.