மத்திய வரம்பு தேற்றம் (வரையறை, ஃபார்முலா) | கணக்கீடுகள் மற்றும் எடுத்துக்காட்டுகள்
மத்திய வரம்பு தேற்றம் வரையறை
எந்தவொரு வரம்பையும் கொண்ட மக்கள்தொகை சீரற்ற மாறியின் சீரற்ற மாதிரிகள் மாதிரியின் அளவு அதிகரிக்கும் போது ஒரு சாதாரண நிகழ்தகவு விநியோகமாக இருக்கும் என்று மத்திய வரம்பு தேற்றம் கூறுகிறது, மேலும் இது மக்கள்தொகையில் மாதிரியின் அளவு 30 ஐ தாண்டும்போது, சராசரி மாதிரியின் அனைத்து அவதானிப்புகளின் சராசரி மக்கள்தொகையின் சராசரிக்கு சமமாக இருக்கும்.
மத்திய வரம்பு தேற்றம் ஃபார்முலா
மாதிரி அளவு 30 ஐத் தாண்டும் போது, விநியோகம் ஒரு சாதாரண விநியோகத்தின் வடிவத்தை எடுக்கும் என்பதை நாங்கள் ஏற்கனவே விவாதித்தோம். ஒரு மாறியின் இயல்பான விநியோகத்தை தீர்மானிக்க, அதன் சராசரி மற்றும் அதன் மாறுபாட்டை அறிந்து கொள்வது அவசியம். ஒரு சாதாரண விநியோகம் எனக் கூறலாம்
X ~ N (, α)
எங்கே
- N = அவதானிப்புகள் இல்லை
- µ = அவதானிப்புகளின் சராசரி
- α = நிலையான விலகல்
பெரும்பாலான சந்தர்ப்பங்களில், அவதானிப்புகள் அதன் மூல வடிவத்தில் அதிகம் வெளிப்படுத்தவில்லை. எனவே அதை ஒப்பிட்டுப் பார்க்கும் வகையில் அவதானிப்புகளை தரப்படுத்துவது மிகவும் முக்கியம். இது z- மதிப்பெண்ணின் உதவியுடன் செய்யப்படுகிறது. ஒரு கண்காணிப்புக்கு இசட் மதிப்பெண்ணைக் கணக்கிட வேண்டும். Z- மதிப்பெண்ணைக் கணக்கிடுவதற்கான சூத்திரம்
Z = (X- µ) / α / .n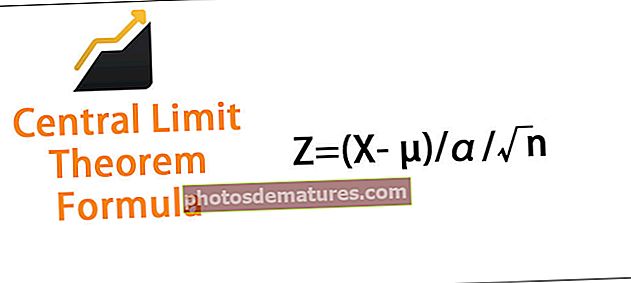
எங்கே
- அவதானிப்புகளின் Z = Z- மதிப்பெண்
- µ = அவதானிப்புகளின் சராசரி
- α = நிலையான விலகல்
- n = மாதிரி அளவு
விளக்கம்
எந்தவொரு வரம்பையும் கொண்ட மக்கள்தொகை சீரற்ற மாறியின் சீரற்ற மாதிரிகள் மாதிரியின் அளவு அதிகரிக்கும்போது சாதாரண நிகழ்தகவு விநியோகமாக இருக்கும் என்று மத்திய வரம்பு தேற்றம் கூறுகிறது. மக்கள்தொகையில் மாதிரியின் அளவு 30 ஐத் தாண்டும்போது, மாதிரியின் சராசரி, மாதிரியின் அனைத்து அவதானிப்புகளின் சராசரி மக்கள்தொகையின் சராசரிக்கு சமமாக இருக்கும் என்று மத்திய வரம்பு தேற்றம் கருதுகிறது. மேலும், மாதிரியின் அளவு 30 ஐத் தாண்டும் போது மாதிரியின் நிலையான விலகல் மக்கள்தொகையின் நிலையான விலகலுக்கு சமமாக இருக்கும். முழு மக்களிடமிருந்தும் மாதிரி தோராயமாக தேர்வு செய்யப்பட்டு, மாதிரியின் அளவு 30 க்கும் அதிகமாக இருப்பதால், இது கருதுகோள் சோதனைக்கு உதவுகிறது மற்றும் கருதுகோள் சோதனைக்கான நம்பிக்கை இடைவெளியை உருவாக்குகிறது.
மத்திய வரம்பு தேற்றம் ஃபார்முலாவின் எடுத்துக்காட்டுகள் (எக்செல் வார்ப்புருவுடன்)
இந்த மத்திய வரம்பு தேற்றம் ஃபார்முலா எக்செல் வார்ப்புருவை இங்கே பதிவிறக்கம் செய்யலாம் - மத்திய வரம்பு தேற்றம் ஃபார்முலா எக்செல் வார்ப்புருஎடுத்துக்காட்டு # 1
ஒரு உதாரணத்தின் உதவியுடன் சாதாரண விநியோகத்தின் கருத்தை புரிந்துகொள்வோம். மியூச்சுவல் ஃபண்டிலிருந்து சராசரி வருவாய் 12%, மற்றும் மியூச்சுவல் ஃபண்ட் முதலீட்டிற்கான சராசரி வருவாயிலிருந்து நிலையான விலகல் 18% ஆகும். பரஸ்பர நிதியத்தின் முதலீட்டில் வருமானத்திற்கான விநியோகத்தை விளக்குவதை விட, வருவாயின் விநியோகம் பொதுவாக விநியோகிக்கப்படுகிறது என்று நாம் கருதினால்.
கொடுக்கப்பட்ட,
- முதலீட்டிற்கான சராசரி வருமானம் 12% ஆக இருக்கும்
- நிலையான விலகல் 18% ஆக இருக்கும்

எனவே, 95% நம்பிக்கை இடைவெளிக்கான வருவாயைக் கண்டறிய, சமன்பாட்டைத் தீர்ப்பதன் மூலம் அதைக் கண்டுபிடிக்கலாம்

- மேல் வரம்பு = 12 + 1.96 (18) = 47%
- கீழ் வீச்சு = 12 - 1.96 (18) = -23%
முடிவு மியூச்சுவல் ஃபண்டிலிருந்து கிடைக்கும் வருமானத்தில் 95% 47% முதல் -23% வரம்பில் இருக்கும் என்பதைக் குறிக்கிறது. இந்த எடுத்துக்காட்டில், 30 க்கும் மேற்பட்ட அவதானிப்புகளின் சீரற்ற மாதிரியின் வருவாயான மாதிரி அளவு, பரஸ்பர நிதியின் மக்கள் தொகை வருவாயின் முடிவை எங்களுக்கு வழங்கும், ஏனெனில் மாதிரி விநியோகம் பொதுவாக விநியோகிக்கப்படும்.
எடுத்துக்காட்டு # 2
அதே எடுத்துக்காட்டுடன் தொடர்ந்தால், 90% நம்பிக்கை இடைவெளியின் விளைவாக என்ன இருக்கும் என்பதை தீர்மானிப்போம்
கொடுக்கப்பட்ட,
- முதலீட்டிற்கான சராசரி வருமானம் 12% ஆக இருக்கும்
- நிலையான விலகல் 18% ஆக இருக்கும்

எனவே, 90% நம்பிக்கை இடைவெளிக்கான வருவாயைக் கண்டறிய, சமன்பாட்டைத் தீர்ப்பதன் மூலம் அதைக் கண்டுபிடிக்கலாம்

- மேல் வரம்பு = 12 + 1.65 (18) = 42%
- கீழ் வீச்சு = 12 - 1.65 (18) = -18%
இதன் விளைவாக மியூச்சுவல் ஃபண்டிலிருந்து கிடைக்கும் வருமானத்தில் 90% 42% முதல் -18% வரம்பில் இருக்கும் என்பதைக் குறிக்கிறது.
எடுத்துக்காட்டு # 3
அதே எடுத்துக்காட்டுடன் தொடர்ந்தால், 99% நம்பிக்கை இடைவெளியின் விளைவு என்ன என்பதை தீர்மானிப்போம்
கொடுக்கப்பட்ட,
- முதலீட்டிற்கான சராசரி வருமானம் 12% ஆக இருக்கும்
- நிலையான விலகல் 18% ஆக இருக்கும்

எனவே, 90% நம்பிக்கை இடைவெளிக்கான வருவாயைக் கண்டறிய, சமன்பாட்டைத் தீர்ப்பதன் மூலம் அதைக் கண்டுபிடிக்கலாம்

- மேல் வரம்பு = 12 + 2.58 (18) = 58%
- கீழ் வீச்சு = 12 - 2.58 (18) = -34%
மியூச்சுவல் ஃபண்டிலிருந்து கிடைக்கும் வருமானத்தில் 99% 58% முதல் -34% வரம்பில் இருக்கும் என்பதை இதன் விளைவாக குறிக்கிறது.
பொருத்தமும் பயன்பாடும்
மைய வரம்பு தேற்றம் மிகவும் பயனுள்ளதாக இருக்கிறது, ஏனெனில் இது மாதிரியின் உதவியுடன் முழு மக்கள்தொகையின் சராசரி மற்றும் நிலையான விலகலை கணிக்க ஆராய்ச்சியாளரை அனுமதிக்கிறது. மாதிரி முழு மக்களிடமிருந்தும் தோராயமாக தேர்வு செய்யப்பட்டு, மாதிரியின் அளவு 30 க்கும் அதிகமாக இருப்பதால், மக்களிடமிருந்து எடுக்கப்பட்ட எந்த சீரற்ற மாதிரி அளவும் பொதுவாக விநியோகிக்கப்படுவதை அணுகும், இது கருதுகோள் சோதனை மற்றும் கருதுகோளின் நம்பிக்கை இடைவெளியை உருவாக்க உதவும். சோதனை. மத்திய வரம்பு தேற்றத்தின் அடிப்படையில், ஆராய்ச்சியாளர் முழு மக்களிடமிருந்தும் எந்தவொரு சீரற்ற மாதிரியையும் தேர்வு செய்ய முடியும், மேலும் மாதிரியின் அளவு 30 ஐ விட அதிகமாக இருக்கும்போது, மாதிரியைப் பின்பற்றுவதால் மாதிரியின் உதவியுடன் மக்கள்தொகையை கணிக்க முடியும். ஒரு சாதாரண விநியோகம் மற்றும் மாதிரியின் சராசரி மற்றும் நிலையான விலகல் மக்கள்தொகையின் சராசரி மற்றும் நிலையான விலகலுக்கு சமமாக இருக்கும்.