மாதிரி பிழை ஃபார்முலா | எடுத்துக்காட்டுகளுடன் படி கணக்கீடு
மாதிரி பிழையை கணக்கிட ஃபார்முலா
மாதிரி பிழை சூத்திரம் சோதனையை நடத்தும் நபர் முழு மக்கள்தொகையையும் கருத்தில் கொண்ட மாதிரியைத் தேர்ந்தெடுக்காத சூழ்நிலையில் நிகழும் புள்ளிவிவரப் பிழையைக் கணக்கிடுவதற்குப் பயன்படுத்தப்படும் சூத்திரத்தைக் குறிக்கிறது மற்றும் சூத்திரத்தின் படி மாதிரி பிழை கணக்கிடப்படுகிறது நிலையான விலகலைப் பிரிப்பதன் மூலம் கணக்கிடப்படுகிறது மாதிரியின் அளவின் சதுர மூலத்தின் மூலம் மக்கள் தொகை, அதன் விளைவாக நம்பக இடைவெளியை அடிப்படையாகக் கொண்ட Z மதிப்பெண் மதிப்புடன் பெருக்கப்படுகிறது.
மாதிரி பிழை = Z x (σ /√n)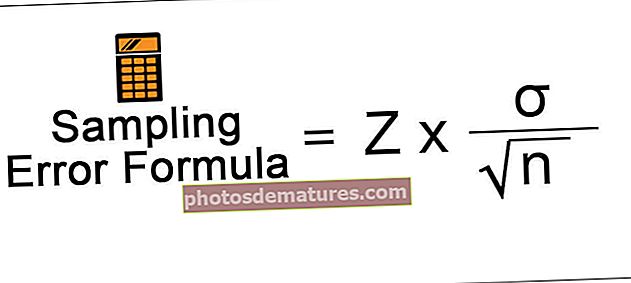
எங்கே,
- Z என்பது நம்பிக்கை இடைவெளியின் அடிப்படையில் Z மதிப்பெண் மதிப்பு
- standard என்பது மக்கள் தொகை நியமச்சாய்வு
- n என்பது மாதிரியின் அளவு
மாதிரி பிழையின் படி கணக்கீடு
- படி 1: மக்கள் தொகை எனப்படும் அனைத்து தரவுகளையும் சேகரித்தது. மக்கள்தொகை வழிமுறைகளையும் மக்கள்தொகை நிலையான விலகலையும் கணக்கிடுங்கள்.
- படி 2: இப்போது, ஒருவர் மாதிரியின் அளவை தீர்மானிக்க வேண்டும், மேலும் மாதிரி அளவு மக்கள்தொகையை விட குறைவாக இருக்க வேண்டும், அது அதிகமாக இருக்கக்கூடாது.
- படி 3: நம்பிக்கை அளவைத் தீர்மானித்தல், அதன்படி ஒருவர் அதன் அட்டவணையில் இருந்து இசட் மதிப்பெண்ணின் மதிப்பை தீர்மானிக்க முடியும்.
- படி 4: இப்போது மக்கள்தொகை நிலையான விலகலால் Z மதிப்பெண்ணைப் பெருக்கி, பிழை அல்லது மாதிரி அளவு பிழையின் விளிம்பில் வருவதற்கு மாதிரி அளவின் சதுர மூலத்தால் அதைப் பிரிக்கவும்.
எடுத்துக்காட்டுகள்
இந்த மாதிரி பிழை ஃபார்முலா எக்செல் வார்ப்புருவை இங்கே பதிவிறக்கம் செய்யலாம் - மாதிரி பிழை ஃபார்முலா எக்செல் வார்ப்புருஎடுத்துக்காட்டு # 1
மக்கள்தொகை நிலையான விலகல் 0.30 மற்றும் மாதிரியின் அளவு 100 என வைத்துக்கொள்வோம். 95% நம்பிக்கை மட்டத்தில் மாதிரி பிழை என்னவாக இருக்கும்?
தீர்வு
இங்கே நமக்கு மக்கள்தொகை நிலையான விலகல் மற்றும் மாதிரியின் அளவு வழங்கப்படுகிறது, எனவே கீழேயுள்ள சூத்திரத்தைப் பயன்படுத்தி அதைக் கணக்கிடலாம்.
கணக்கீட்டிற்கு பின்வரும் தரவைப் பயன்படுத்தவும்.

எனவே, மாதிரி பிழையின் கணக்கீடு பின்வருமாறு,

மாதிரி பிழை இருக்கும் -

எடுத்துக்காட்டு # 2
க ut தம் தற்போது கணக்கியல் படிப்பைத் தொடர்கிறார், அவர் நுழைவுத் தேர்வில் தேர்ச்சி பெற்றுள்ளார். அவர் இப்போது ஒரு இடைநிலை நிலைக்கு பதிவு செய்துள்ளார், மேலும் ஒரு மூத்த கணக்காளரை ஒரு பயிற்சியாளராக சேர்ப்பார். அவர் உற்பத்தி நிறுவனங்களின் தணிக்கை செய்வார்.
அவர் முதன்முறையாக வருகை தந்த நிறுவனங்களில் ஒன்று, வாங்குவதற்கான அனைத்து உள்ளீடுகளுக்கான பில்கள் நியாயமான முறையில் கிடைக்குமா என்று சோதிக்கும்படி கேட்கப்பட்டது. அவர் எடுத்த மாதிரி அளவு 50 ஆகவும், அதற்கான மக்கள்தொகை நியமச்சாய்வு 0.50 ஆகவும் இருந்தது.
கிடைக்கக்கூடிய தகவல்களின் அடிப்படையில், நீங்கள் மாதிரி பிழையை 95% மற்றும் 99% நம்பிக்கை இடைவெளியில் கணக்கிட வேண்டும்.
தீர்வு
இங்கே நமக்கு மக்கள்தொகை நிலையான விலகல் மற்றும் மாதிரியின் அளவு வழங்கப்படுகிறது, எனவே கீழேயுள்ள சூத்திரத்தைப் பயன்படுத்தி அதைக் கணக்கிடலாம்.
95% நம்பிக்கை நிலைக்கு Z மதிப்பெண் 1.96 ஆக இருக்கும் (Z மதிப்பெண் அட்டவணையில் இருந்து கிடைக்கும்)
கணக்கீட்டிற்கு பின்வரும் தரவைப் பயன்படுத்தவும்.

எனவே, கணக்கீடு பின்வருமாறு,

மாதிரி பிழை இருக்கும் -

95% நம்பிக்கை நிலைக்கு Z மதிப்பெண் 2.58 ஆக இருக்கும் (Z மதிப்பெண் அட்டவணையில் இருந்து கிடைக்கும்)
கணக்கீட்டிற்கு பின்வரும் தரவைப் பயன்படுத்தவும்.

எனவே, கணக்கீடு பின்வருமாறு,

மாதிரி பிழை இருக்கும் -

நம்பிக்கை நிலை அதிகரிக்கும்போது, மாதிரி பிழையும் அதிகரிக்கிறது.
எடுத்துக்காட்டு # 3
ஒரு பள்ளியில், மாணவர்களின் ஆரோக்கியத்தை சரிபார்க்க பயோமெட்ரிக் அமர்வு ஏற்பாடு செய்யப்பட்டது. அமர்வு பத்தாம் வகுப்பு மாணவர்களுடன் தொடங்கப்பட்டது. பி பிரிவில் மொத்தம் 30 மாணவர்கள் உள்ளனர். அவர்களில் 12 மாணவர்கள் தோராயமாக விவரங்களைச் சரிபார்க்க தேர்வு செய்யப்பட்டனர், மீதமுள்ளவர்கள், ஒரே ஒரு அடிப்படை சோதனை செய்யப்பட்டது. பி பிரிவில் உள்ள மாணவர்களின் சராசரி உயரம் 154 என்று அறிக்கை ஊகித்துள்ளது.

தீர்வு
மக்கள்தொகை நியமச்சாய்வு 9.39 ஆகும். மேலே உள்ள தகவலின் அடிப்படையில், நீங்கள் 90% மற்றும் 95% நம்பிக்கை இடைவெளியில் மாதிரி பிழையை கணக்கிட வேண்டும்.
இங்கே நமக்கு மக்கள்தொகை நிலையான விலகல் மற்றும் மாதிரியின் அளவு வழங்கப்படுகிறது, எனவே கீழேயுள்ள சூத்திரத்தைப் பயன்படுத்தி அதைக் கணக்கிடலாம்.
95% நம்பிக்கை நிலைக்கு Z மதிப்பெண் 1.96 ஆக இருக்கும் (Z மதிப்பெண் அட்டவணையில் இருந்து கிடைக்கும்)
கணக்கீட்டிற்கு பின்வரும் தரவைப் பயன்படுத்தவும்.

எனவே, மாதிரி பிழையின் கணக்கீடு பின்வருமாறு,

மாதிரி பிழை இருக்கும் -

90% நம்பிக்கை நிலைக்கு Z மதிப்பெண் 1.645 ஆக இருக்கும் (Z மதிப்பெண் அட்டவணையில் இருந்து கிடைக்கும்)
கணக்கீட்டிற்கு பின்வரும் தரவைப் பயன்படுத்தவும்.

எனவே, கணக்கீடு பின்வருமாறு,

மாதிரி பிழை இருக்கும் -

நம்பிக்கை நிலை குறையும்போது, மாதிரி பிழையும் குறைகிறது.
சம்பந்தம் மற்றும் பயன்கள்
இந்த கருத்தை புரிந்து கொள்ள இது மிகவும் முக்கியமானது, ஏனெனில் கணக்கெடுப்பு முடிவுகள் உண்மையில் ஒட்டுமொத்த மக்கள்தொகையின் உண்மையான பார்வையை சித்தரிக்கும் என்று ஒருவர் எவ்வளவு எதிர்பார்க்கலாம் என்பதை இது சித்தரிக்கும். ஒரு பெரிய மக்கள்தொகையை பிரதிநிதித்துவப்படுத்த மாதிரி அளவு (கணக்கெடுப்பின் பதிலளித்தவர்கள் என புகழ்பெற்றது) எனப்படும் சிறிய மக்கள்தொகையைப் பயன்படுத்தி ஒரு கணக்கெடுப்பு செய்யப்படுகிறது என்பதை ஒருவர் மனதில் கொள்ள வேண்டும்.
கணக்கெடுப்பின் செயல்திறனைக் கணக்கிடுவதற்கான ஒரு வழியாக இதைப் பார்க்கலாம். மாதிரி விளிம்பு அதிகமாக இருக்கும்போது, கணக்கெடுப்பு விளைவுகள் உண்மையான மொத்த மக்கள் பிரதிநிதித்துவத்திலிருந்து விலகிச் செல்லக்கூடும் என்பதைக் குறிக்கும். மறுபுறம், ஒரு மாதிரி பிழை அல்லது பிழையின் விளிம்பு அதை விட சிறியது, இதன் விளைவுகள் இப்போது மொத்த மக்கள்தொகையின் உண்மையான பிரதிநிதித்துவத்துடன் நெருக்கமாக இருப்பதைக் குறிக்கும், மேலும் இது பார்வையில் இருக்கும் கணக்கெடுப்பு பற்றிய உயர் மட்ட நம்பிக்கையை உருவாக்கும்.