பல பின்னடைவு சூத்திரம் | பல பின்னடைவு சமன்பாட்டின் கணக்கீடு
பல பின்னடைவு சூத்திரம் என்றால் என்ன?
சார்பு மற்றும் பல சுயாதீன மாறிகளுக்கு இடையிலான உறவின் பகுப்பாய்வில் பல பின்னடைவு சூத்திரம் பயன்படுத்தப்படுகிறது மற்றும் சூத்திரம் Y சமன்பாட்டால் குறிக்கப்படுகிறது ஒரு பிளஸ் பிஎக்ஸ் 1 மற்றும் சிஎக்ஸ் 2 பிளஸ் டிஎக்ஸ் 3 பிளஸ் ஈ சமம், அங்கு ஒய் சார்பு மாறி, எக்ஸ் 1, எக்ஸ் 2, எக்ஸ் 3 சுயாதீன மாறிகள் , a என்பது இடைமறிப்பு, b, c, d ஆகியவை சரிவுகளாகும், மற்றும் E என்பது மீதமுள்ள மதிப்பு.
y = mx1 + mx2 + mx3 + b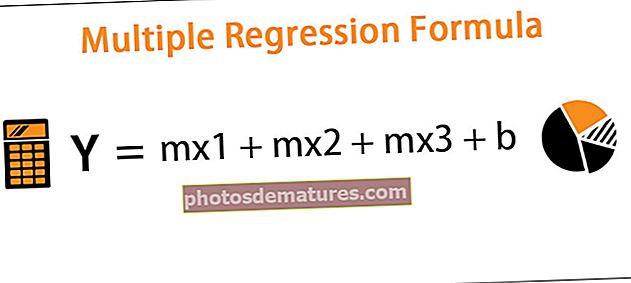
எங்கே,
- Y = பின்னடைவின் சார்பு மாறி
- எம் = பின்னடைவின் சாய்வு
- எக்ஸ் 1 = பின்னடைவின் முதல் சுயாதீன மாறி
- பின்னடைவின் x2 = இரண்டாவது சுயாதீன மாறி
- பின்னடைவின் x3 = மூன்றாவது சுயாதீன மாறி
- பி = மாறிலி
பின்னடைவு பகுப்பாய்வு சூத்திரத்தின் விளக்கம்
பல பின்னடைவுகள் என்பது இரண்டு அல்லது அதற்கு மேற்பட்ட சுயாதீன மாறிகளின் உதவியுடன் சார்பு மாறியைக் கணிப்பதற்கான ஒரு முறையாகும். இந்த பகுப்பாய்வை இயக்கும் போது, ஆராய்ச்சியாளரின் முக்கிய நோக்கம் சார்பு மாறி மற்றும் சுயாதீன மாறிகளுக்கு இடையிலான உறவைக் கண்டுபிடிப்பதாகும். சார்பு மாறியைக் கணிக்க, பல சுயாதீன மாறிகள் தேர்ந்தெடுக்கப்படுகின்றன, அவை சார்பு மாறியைக் கணிக்க உதவும். நேரியல் பின்னடைவு நோக்கத்திற்காக சேவை செய்ய முடியாதபோது இது பயன்படுத்தப்படுகிறது. பின்னடைவு பகுப்பாய்வு, சார்பு மாறியைக் கணிக்க உதவுவதற்கு முன்னறிவிப்பு மாறிகள் போதுமானதா என்பதை சரிபார்க்கும் செயல்பாட்டில் உதவுகிறது.
எடுத்துக்காட்டுகள்
இந்த பல பின்னடைவு ஃபார்முலா எக்செல் வார்ப்புருவை இங்கே பதிவிறக்கம் செய்யலாம் - பல பின்னடைவு ஃபார்முலா எக்செல் வார்ப்புருஎடுத்துக்காட்டு # 1
ஒரு உதாரணத்தின் உதவியுடன் பல பின்னடைவு பகுப்பாய்வின் கருத்தை முயற்சித்துப் புரிந்துகொள்வோம். யுபிஆர் இயக்கி உள்ளடக்கிய தூரம் மற்றும் ஓட்டுநரின் வயது மற்றும் ஓட்டுநரின் அனுபவத்தின் எண்ணிக்கை ஆகியவற்றுக்கு என்ன தொடர்பு என்று கண்டுபிடிக்க முயற்சிப்போம்.

பல பின்னடைவின் கணக்கீட்டிற்கு எக்செல் உள்ள தரவு தாவலுக்குச் சென்று பின்னர் தரவு பகுப்பாய்வு விருப்பத்தைத் தேர்ந்தெடுக்கவும். மேலதிக செயல்முறை மற்றும் கணக்கீடு இங்கே கொடுக்கப்பட்ட கட்டுரையை குறிக்கிறது - எக்செல் இல் பகுப்பாய்வு கருவிப்பட்டி

மேலே உள்ள எடுத்துக்காட்டுக்கான பின்னடைவு சூத்திரம் இருக்கும்
- y = MX + MX + b
- y = 604.17 * -3.18 + 604.17 * -4.06 + 0
- y = -4377
இந்த குறிப்பிட்ட எடுத்துக்காட்டில், எந்த மாறி சார்பு மாறி மற்றும் எந்த மாறி சுயாதீன மாறி என்று பார்ப்போம். இந்த பின்னடைவு சமன்பாட்டின் சார்பு மாறி என்பது யுபிஆர் இயக்கி உள்ளடக்கிய தூரம் மற்றும் சுயாதீன மாறிகள் என்பது ஓட்டுநரின் வயது மற்றும் அவர் வாகனம் ஓட்டுவதில் அனுபவங்களின் எண்ணிக்கை.
எடுத்துக்காட்டு # 2
மற்றொரு பின்னணியின் உதவியுடன் பல பின்னடைவு பகுப்பாய்வின் கருத்தை முயற்சித்துப் புரிந்துகொள்வோம். ஒரு வகுப்பின் மாணவர்களின் ஜி.பி.ஏ மற்றும் படிப்பு மணிநேரம் மற்றும் மாணவர்களின் உயரம் ஆகியவற்றுக்கு என்ன தொடர்பு என்று கண்டுபிடிக்க முயற்சிப்போம்.

கணக்கீட்டிற்கு, எக்செல் உள்ள தரவு தாவலுக்குச் சென்று பின்னர் தரவு பகுப்பாய்வு விருப்பத்தைத் தேர்ந்தெடுக்கவும்.

மேலே உள்ள உதாரணத்திற்கான பின்னடைவு சமன்பாடு இருக்கும்
y = MX + MX + b
y = 1.08 * .03 + 1.08 * -. 002 + 0
y = .0325
இந்த குறிப்பிட்ட எடுத்துக்காட்டில், எந்த மாறி சார்பு மாறி மற்றும் எந்த மாறி சுயாதீன மாறி என்று பார்ப்போம். இந்த பின்னடைவில் சார்பு மாறி ஜி.பி.ஏ மற்றும் சுயாதீன மாறிகள் படிப்பு நேரம் மற்றும் மாணவர்களின் உயரம்.
எடுத்துக்காட்டு # 3
மற்றொரு பின்னணியின் உதவியுடன் பல பின்னடைவு பகுப்பாய்வின் கருத்தை முயற்சித்துப் புரிந்துகொள்வோம். ஒரு நிறுவனத்தில் பணியாற்றும் ஒரு குழுவினரின் சம்பளத்திற்கும் அனுபவத்தின் எண்ணிக்கைக்கும் ஊழியர்களின் வயதுக்கும் என்ன தொடர்பு என்று கண்டுபிடிக்க முயற்சிப்போம்.

கணக்கீட்டிற்கு, எக்செல் உள்ள தரவு தாவலுக்குச் சென்று பின்னர் தரவு பகுப்பாய்வு விருப்பத்தைத் தேர்ந்தெடுக்கவும்.

மேலே உள்ள உதாரணத்திற்கான பின்னடைவு சமன்பாடு இருக்கும்
- y = MX + MX + b
- y = 41308 * .- 71 + 41308 * -824 + 0
- y = -37019
இந்த குறிப்பிட்ட எடுத்துக்காட்டில், எந்த மாறி சார்பு மாறி மற்றும் எந்த மாறி சுயாதீன மாறி என்று பார்ப்போம். இந்த பின்னடைவு சமன்பாட்டின் சார்பு மாறி சம்பளம் மற்றும் சுயாதீன மாறிகள் என்பது ஊழியர்களின் அனுபவம் மற்றும் வயது.
பொருத்தமும் பயன்பாடும்
பல பின்னடைவுகள் மிகவும் பயனுள்ள புள்ளிவிவர முறையாகும். நிதி உலகில் பின்னடைவு மிகவும் பங்கு வகிக்கிறது. பின்னடைவு பகுப்பாய்வைப் பயன்படுத்தி நிறைய முன்கணிப்பு செய்யப்படுகிறது. எடுத்துக்காட்டாக, ஒரு குறிப்பிட்ட பிரிவின் விற்பனையை மேக்ரோ பொருளாதார குறிகாட்டிகளின் உதவியுடன் முன்கூட்டியே கணிக்க முடியும், அது அந்த பகுதியுடன் நல்ல தொடர்பைக் கொண்டுள்ளது.