எக்செல் இல் SIN (ஃபார்முலா, எடுத்துக்காட்டுகள்) | எக்செல் இல் பாவ செயல்பாட்டை எவ்வாறு பயன்படுத்துவது?
SIN எக்செல் செயல்பாடு என்பது எக்செல் இல் உள்ளடிக்கப்பட்ட முக்கோணவியல் செயல்பாடு ஆகும், இது கொடுக்கப்பட்ட எண்ணின் சைன் மதிப்பைக் கணக்கிட அல்லது ஒரு குறிப்பிட்ட கோணத்தின் சைன் மதிப்பை முக்கோணவியல் அடிப்படையில் பயன்படுத்த பயன்படுகிறது, இங்கே கோணம் எக்செல் இல் ஒரு எண் மற்றும் இந்த செயல்பாடு ஒரு வாதத்தை மட்டுமே எடுக்கும் இது வழங்கப்பட்ட உள்ளீட்டு எண்.
எக்செல் இல் SIN செயல்பாடு
எக்செல் இல் உள்ள SIN செயல்பாடு நாம் குறிப்பிடும் ஒரு கோணத்தின் சைனைக் கணக்கிடுகிறது. எக்செல் செயல்பாட்டில் உள்ள SIN எக்செல் இல் கணித / முக்கோணவியல் செயல்பாடாக வகைப்படுத்தப்படுகிறது. எக்செல் உள்ள SIN எப்போதும் ஒரு எண் மதிப்பை வழங்குகிறது.
கணிதம் மற்றும் முக்கோணவியல் ஆகியவற்றில், SINE என்பது ஒரு கோணத்தின் முக்கோணவியல் செயல்பாடாகும், இது ஒரு வலது கோண முக்கோணத்தில் எதிர் பக்கத்தின் நீளத்திற்கு (வலது கோண பக்கத்திற்கு) சமமாக இருக்கும், இது ஹைப்போடனஸின் நீளத்தால் வகுக்கப்படுகிறது, :
பாவம் Θ = எதிர் பக்கம் / ஹைபோடென்யூஸ்

பாவம் Θ = அ / ம
எக்செல் இல் SIN ஃபார்முலா
எக்செல் இல் உள்ள SIN ஃபார்முலா கீழே உள்ளது.

எண் என்பது ரேடியன்களில் SIN ஃபார்முலாவுக்கு அனுப்பப்படும் ஒரு வாதம்.
எக்செல் செயல்பாட்டில் நாம் நேரடியாக SIN க்கு கோணத்தை அனுப்பினால், அது சரியான வாதமாக அங்கீகரிக்கப்படாது. எடுத்துக்காட்டாக, எக்செல் செயல்பாட்டில் இந்த SIN க்கு வாதமாக 30 pass ஐ கடந்துவிட்டால், அது சரியான வாதமாக அங்கீகரிக்கப்படாது. எக்செல் பிழை செய்தியைக் காண்பிக்கும்.

எனவே, நாம் கடந்து செல்ல வேண்டிய வாதம் இருக்க வேண்டும் ரேடியன்கள்.
ஒரு கோணத்தை ரேடியனாக மாற்ற, இரண்டு முறைகள் உள்ளன
- உள்ளடிக்கிய எக்செல் ரேடியன்ஸ் செயல்பாட்டைப் பயன்படுத்தவும். RADIANS செயல்பாடு டிகிரிகளை ஒரு ரேடியன் மதிப்பாக மாற்றுகிறது.
எடுத்துக்காட்டாக, 30 radi ஐ ரேடியனாக மாற்ற இந்த செயல்பாட்டைப் பயன்படுத்துவோம், இது பட்டம் ஒரு எண்ணாக எடுக்கும், அது 30 30 ஆக 30 ஆக இருக்கும்.
=ரேடியன்ஸ் (30) ரேடியன் 0.52 ஐ வழங்கும்

- இரண்டாவது வழக்கில் நாம் ஒரு பட்டம் ரேடியனாக மாற்ற கணித சூத்திரத்தைப் பயன்படுத்தலாம். ஃபார்முலா உள்ளது
ரேடியன் = டிகிரி * (π / 180) (π = 3.14)
எக்செல் இல் பை இன் மதிப்பை 15 இலக்கங்களுக்கு துல்லியமாக வழங்கும் ஒரு செயல்பாடும் உள்ளது, மேலும் செயல்பாடு உள்ளது பிஐ ()
எனவே, ரேடியன் மாற்றத்திற்கு பட்டம் பெற, நாங்கள் சூத்திரத்தைப் பயன்படுத்துவோம்
ரேடியன் = டிகிரி * (பிஐ () / 180)
எக்செல் இல் SIN செயல்பாட்டை எவ்வாறு பயன்படுத்துவது?
எக்செல் இல் SIN செயல்பாடு மிகவும் எளிமையானது மற்றும் பயன்படுத்த எளிதானது. சில எடுத்துக்காட்டுகள் மூலம் எக்செல் இல் SIN இன் செயல்பாட்டைப் புரிந்துகொள்வோம்.
எக்செல் வார்ப்புருவில் இந்த SIN ஐ இங்கே பதிவிறக்கம் செய்யலாம் - எக்செல் வார்ப்புருவில் SINஎக்செல் எடுத்துக்காட்டு # 1 இல் உள்ள SIN
எக்செல் இல் SIN செயல்பாடு மற்றும் எக்செல் இல் RADIANS செயல்பாட்டைப் பயன்படுத்தி சைன் மதிப்பைக் கணக்கிடுகிறது எக்செல் மற்றும் பிஐ செயல்பாட்டில் SIN செயல்பாட்டைப் பயன்படுத்தி சைன் மதிப்பைக் கணக்கிடுகிறது எக்செல் இல் சைன் செயல்பாடு பல நிஜ வாழ்க்கை பயன்பாடுகளைக் கொண்டுள்ளது; வடிவியல் புள்ளிவிவரங்களின் உயரங்களையும் நீளங்களையும் கணக்கிட இது கட்டிடக்கலைகளில் பரவலாகப் பயன்படுத்தப்படுகிறது. அட்சரேகை மற்றும் தீர்க்கரேகை புவியியல் இருப்பிடம், வானொலி ஒலிபரப்பு போன்றவற்றின் அடிப்படையில் குறுகிய பாதையைக் கண்டறிய ஜி.பி.எஸ், ஒளியியல், பாதைகளை கணக்கிடுதல் போன்றவற்றிலும் இது பயன்படுத்தப்படுகிறது. ஒரு மின்காந்த அலை கூட சைன் மற்றும் கொசைன் செயல்பாட்டின் வரைபடமாக திட்டமிடப்பட்டுள்ளது. எங்களிடம் மூன்று வலது கோண முக்கோணங்கள் உள்ளன, அவற்றின் கோணங்களும் ஒரு பக்கத்தின் நீளமும் கொடுக்கப்பட்டுள்ளன, மற்ற இரு பக்கங்களின் நீளத்தையும் நாம் கணக்கிட வேண்டும். ஒரு முக்கோணத்தின் அனைத்து கோணங்களின் கூட்டுத்தொகை 180 to க்கு சமம், எனவே, மூன்றாவது கோணத்தை எளிதாக கணக்கிடலாம். பாவம் Θ = எதிர் / ஹைபோடென்யூஸ் என்பது எங்களுக்குத் தெரியும் எனவே, எதிர் பக்க நீளம் இருக்கும் பாவம் Θ * ஹைபோடென்யூஸ் எக்செல் இல், எதிரெதிர் பக்கத்தின் நீளம் (செங்குத்தாக), SIN சூத்திரத்தால் கணக்கிடப்படும் = SIN (RADIANS (C2)) * E2 மேலே கொடுக்கப்பட்ட SIN சூத்திரத்தை மூன்று முக்கோணங்களுக்குப் பயன்படுத்தினால் முக்கோணங்களின் செங்குத்துகளின் நீளத்தைப் பெறலாம் மூன்றாம் பக்கத்திற்கு (அருகிலுள்ள பக்கம்), எங்களுக்கு இரண்டு முறைகள் உள்ளன - பித்தகோரஸ் தேற்றத்தைப் பயன்படுத்துவதன் மூலம் அல்லது மற்ற கோணங்களிலிருந்து எக்செல் செயல்பாட்டில் SIN ஐப் பயன்படுத்துவதன் மூலம். பித்தகோரஸ் தேற்றத்தின் படி, வலது கோண முக்கோணத்தின் இரண்டு பக்கங்களின் சதுரங்களின் தொகை ஹைப்போடென்ஸின் சதுரத்திற்கு சமம். ஹைப்போடென்யூஸ் 2 = எதிர் 2 + அருகிலுள்ள 2 அருகிலுள்ள = (ஹைபோடென்யூஸ் 2 - எதிர் 2) 1/2 எக்செல் இல், இதை எழுதுவோம், = POWER ((POWER (Hypotenuse, 2) -POWER (எதிர், 2%), 1/2) இந்த சூத்திரத்தைப் பயன்படுத்துவதன் மூலம், அருகிலுள்ள பக்கத்தின் நீளத்தைக் கணக்கிடுகிறோம் = POWER ((POWER (E2,2) -POWER (F2,2%), 1/2) இரண்டாவது முறையைப் பயன்படுத்தி, அருகிலுள்ள பக்கத்தின் மதிப்பைக் கணக்கிட 3 வது கோணத்தின் SINE ஐப் பயன்படுத்தலாம் நாம் முக்கோணங்களை 90 ° இடதுபுறமாக சுழற்றினால், எதிர் பக்கமானது பக்கவாட்டுடன் மாற்றப்பட்டு, ஹைபோடென்யூஸ் மற்றும் அருகிலுள்ள கோணத்தின் SIN மூன்றாம் பக்கத்தின் மதிப்பைக் கணக்கிட உதவும். = SIN (RADIANS (D2)) * E2 அறியப்படாத உயரத்தின் உயரமான கட்டிடம் உள்ளது மற்றும் ஒரு கட்டத்தில் சூரிய கதிர் 75 A புள்ளியில் ஒரு கோணத்தை உருவாக்குகிறது, இதனால் 70 மீட்டர் நீளமுள்ள கட்டிடத்தின் நிழலை உருவாக்குகிறது. கோபுரத்தின் உயரத்தை நாம் கண்டுபிடிக்க வேண்டும் எக்செல் செயல்பாட்டில் SIN ஐப் பயன்படுத்தி கட்டிடத்தின் உயரம் கணக்கிடப்படும் SIN 75 ° = கட்டடத்தின் உயரம் / நிழலின் நீளம் A புள்ளியில் எனவே, கட்டிடத்தின் உயரம் = SIN 75 ° * புள்ளி A இல் நிழலின் நீளம் எனவே, கட்டிடத்தின் உயரம் இருக்கும் = SIN (RADIANS (B3)) * B2 கட்டிடத்தின் உயரம் 67.61 மீட்டர் எங்களுக்கு ஒரு முக்கோண வடிவத்தில் ஒரு நிலம் உள்ளது, இதற்காக இரு கோணங்களும் 30 ° மற்றும் 70 as என வழங்கப்படுகின்றன, மேலும் முக்கோணத்தின் ஒரு பக்கத்தின் நீளம் 40 மீட்டர் மட்டுமே நமக்குத் தெரியும். மற்ற மூன்று பக்கங்களின் நீளத்தையும் முக்கோணத்தின் சுற்றளவையும் நாம் கண்டுபிடிக்க வேண்டும். ஒரு முக்கோணத்தைப் பொறுத்தவரை, ஒரு பக்கமும் அனைத்து கோணங்களும் அறியப்படும்போது, SINE விதி மூலம் மற்ற பக்கங்களைக் கணக்கிடலாம் முக்கோணவியலில் உள்ள சைன் விதி ஒரு SIN சூத்திரத்தால் பாவி கோணங்கள் மற்றும் ஒரு முக்கோணத்தின் பக்கங்களின் தொடர்பை வழங்குகிறது a / sin α = b / sin ß = c / sin இந்த வழக்கில், α = 30 °, = 70 ° மற்றும் δ = 180 ° - (30 ° + 70 °) = 80 ° மற்றும் முக்கோணத்தின் ஒரு பக்கம் b = 40 மீட்டர் முக்கோணத்தின் மற்ற பக்கங்களைக் கண்டுபிடிக்க நாம் SINE விதியைப் பயன்படுத்துவோம் a = பாவம் α * (ப / பாவம் ß) எனவே, a = SIN (RADIANS (30%) * * (B5 / SIN (RADIANS (70%)) பக்கத்தின் நீளம் a = 21.28 மீட்டர் இதேபோல், மூன்றாம் பக்க சி இருக்கும் c = பாவம் δ * (பி / பாவம் ß) எனவே, c = SIN (RADIANS (80%)) * (B5 / SIN (RADIANS (70%)) முக்கோணத்தின் மூன்று பக்கங்களும் 21.28, 40, 41.92 மீட்டர் நீளம் கொண்டவை. முக்கோணத்தின் சுற்றளவு அனைத்து பக்கங்களின் கூட்டுத்தொகையாகும். எனவே, சுற்றளவு இருக்கும் = SUM (B5: B7)



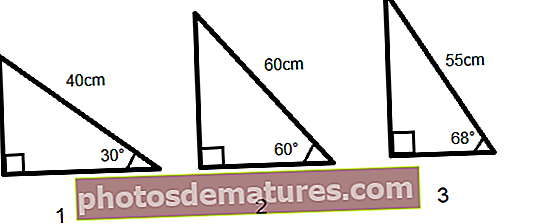








எக்செல் எடுத்துக்காட்டு # 2 இல் SIN



எக்செல் எடுத்துக்காட்டு # 3 இல் SIN