பண சூத்திரத்தின் நேர மதிப்பு | படி கணக்கீடு
பணத்தின் நேர மதிப்பைக் கணக்கிடுவதற்கான சூத்திரம்
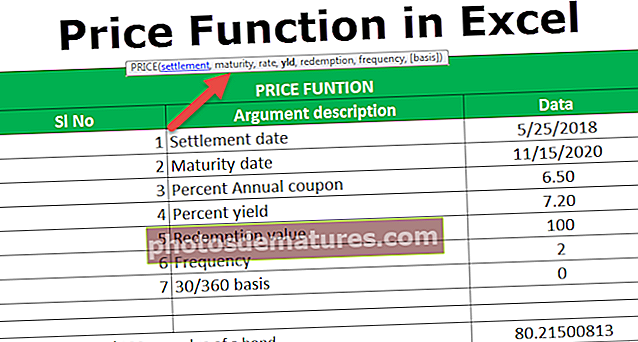
பணத்தின் நேர மதிப்பைக் கணக்கிடுவதற்கான சூத்திரம் (டி.வி.எம்) எதிர்கால பணத்தின் மதிப்பை தற்போதைய மதிப்புக்கு தள்ளுபடி செய்கிறது அல்லது பணத்தின் தற்போதைய மதிப்பை எதிர்கால மதிப்புடன் கூட்டுகிறது. FV = PV * (1 + i / n) n * t அல்லது PV = FV / (1 + i / n) n * t
- FV = பணத்தின் எதிர்கால மதிப்பு,
- பி.வி = பணத்தின் தற்போதைய மதிப்பு,
- i = இதே போன்ற முதலீட்டில் வட்டி விகிதம் அல்லது தற்போதைய மகசூல்,
- t = ஆண்டுகளின் எண்ணிக்கை மற்றும்
- n = வருடத்திற்கு வட்டி கூட்டு காலங்களின் எண்ணிக்கை

பணக் கணக்கீட்டின் நேர மதிப்பு (படிப்படியாக)
- படி 1: முதலாவதாக, சந்தை நிலைமையின் அடிப்படையில் இதேபோன்ற முதலீட்டில் இருந்து எதிர்பார்க்கப்படும் வட்டி வீதம் அல்லது வருவாய் விகிதத்தைக் கண்டுபிடிக்க முயற்சிக்கவும். இங்கே குறிப்பிடப்பட்டுள்ள வட்டி விகிதம் பயனுள்ள வட்டி விகிதம் அல்ல, ஆனால் ஆண்டு வட்டி விகிதம் என்பதை நினைவில் கொள்க. இது குறிக்கப்படுகிறது ‘நான்’.
- படி 2: இப்போது, எண் ஆண்டுகளின் அடிப்படையில் முதலீட்டின் பதவிக்காலம் தீர்மானிக்கப்பட வேண்டும், அதாவது எவ்வளவு காலம் பணம் முதலீடு செய்யப் போகிறது. ஆண்டுகளின் எண்ணிக்கை குறிக்கப்படுகிறது ‘டி’.
- படி 3: இப்போது, வருடத்திற்கு வட்டி கூட்டும் காலங்களின் எண்ணிக்கையை தீர்மானிக்க வேண்டும், அதாவது ஒரு வருடத்தில் எத்தனை முறை வட்டி வசூலிக்கப்படும். வட்டி கூட்டு என்பது காலாண்டு, அரை ஆண்டு, ஆண்டுதோறும் இருக்கலாம். ஆண்டுக்கு வட்டி கூட்டு காலங்களின் எண்ணிக்கை குறிக்கப்படுகிறது ‘n’.
- படி 4: இறுதியாக, பணத்தின் தற்போதைய மதிப்பு (பி.வி) கிடைத்தால், ‘டி’ ஆண்டுக்குப் பிறகு எதிர்கால பணத்தின் மதிப்பு (எஃப்.வி) பின்வரும் சூத்திரத்தைப் பயன்படுத்தி கணக்கிடலாம்,
FV = PV * (1 + i / n) n * t
மறுபுறம், ஆண்டின் ‘டி’ எண்ணுக்குப் பிறகு எதிர்கால பணத்தின் மதிப்பு (எஃப்.வி) கிடைத்தால், இன்றைய பணத்தின் மதிப்பை (பி.வி) இன்று பின்வரும் சூத்திரத்தைப் பயன்படுத்தி கணக்கிடலாம்,
PV = FV / (1 + i / n) n * t
உதாரணமாக
பண எக்செல் வார்ப்புருவின் இந்த நேர மதிப்பை இங்கே பதிவிறக்கம் செய்யலாம் - பண எக்செல் வார்ப்புருவின் நேர மதிப்புஎடுத்துக்காட்டு # 1
இன்று 12% வட்டி விகிதத்தில் இரண்டு ஆண்டுகளாக முதலீடு செய்யப்பட்ட, 000 100,000 தொகையை எடுத்துக்காட்டுவோம். கூட்டு செய்தால் பணத்தின் எதிர்கால மதிப்பைக் கணக்கிடுவோம்:
- மாதாந்திர
- காலாண்டு
- அரையாண்டு
- ஆண்டுதோறும்
கொடுக்கப்பட்டால், பணத்தின் தற்போதைய மதிப்பு (பி.வி) = $ 100,000, நான் = 12%, டி = 2 ஆண்டுகள்
# 1 - மாதாந்திர கூட்டு
மாதந்தோறும், எனவே n = 12
பணத்தின் எதிர்கால மதிப்பு (FV) = $ 100,000 * (1 +) 12 * 2
- FV = $ 126,973.46 ~ $126,973
# 2 - காலாண்டு கூட்டு
காலாண்டு முதல், எனவே n = 4
பணத்தின் எதிர்கால மதிப்பு (FV) = $ 100,000 * (1 +) 4 * 2
- FV = $ 126,677.01 ~ $126,677
# 3 - அரை ஆண்டு கூட்டு
அரை ஆண்டு முதல், எனவே n = 2
பணத்தின் எதிர்கால மதிப்பு (FV) = $ 100,000 * (1 +) 2 * 2
- FV = $ 126,247.70 ~ $126,248
# 4 - வருடாந்திர கூட்டு
ஆண்டுதோறும், எனவே n =
பணத்தின் எதிர்கால மதிப்பு (FV) = $ 100,000 * (1 +) 1 * 2
- FV = $ 125,440.00 ~ $125,440
எனவே, பல்வேறு கூட்டு காலங்களுக்கான பணத்தின் எதிர்கால மதிப்பு -

மேலேயுள்ள எடுத்துக்காட்டு பண சூத்திரத்தின் நேர மதிப்பைக் கணக்கிடுவதைக் காட்டுகிறது, இது வட்டி விகிதம் மற்றும் முதலீட்டின் பதவிக்காலம் மட்டுமல்ல, ஒரு வருடத்தில் எத்தனை முறை வட்டி கூட்டு நிகழ்கிறது என்பதையும் சார்ந்துள்ளது.
எடுத்துக்காட்டு # 2
இரண்டு ஆண்டுகளுக்குப் பிறகு பெறப்பட வேண்டிய, 000 100,000 மற்றும் தள்ளுபடி விகிதம் 10% ஆகும். கூட்டுப்பணி முடிந்தால் இப்போது தற்போதைய மதிப்பைக் கணக்கிடுவோம்.
- மாதாந்திர
- காலாண்டு
- அரையாண்டு
- ஆண்டுதோறும்
கொடுக்கப்பட்டால், FV = $ 100,000, i = 10%, t = 2 ஆண்டுகள்
# 1 - மாதாந்திர கூட்டு
மாதந்தோறும், எனவே n = 12
பணத்தின் தற்போதைய மதிப்பு (பி.வி) = $ 100,000 / (1 +) 12 * 2
- பி.வி = $ 81,940.95 ~ $81,941
#2 – காலாண்டுகூட்டு
காலாண்டு முதல், எனவே n = 4
பணத்தின் தற்போதைய மதிப்பு (பி.வி) = $ 100,000 / (1 +) 4 * 2
- பி.வி = $ 82,074.66 ~ $82,075
#3 – அரையாண்டுகூட்டு
அரை ஆண்டு முதல், எனவே n = 2
பணத்தின் தற்போதைய மதிப்பு (பி.வி) = $ 100,000 / (1 +) 2 * 2
- பி.வி = $ 82,270.25 ~ $82,270
#4 – ஆண்டுகூட்டு
ஆண்டுதோறும், எனவே n =
பணத்தின் தற்போதைய மதிப்பு (பி.வி) = $ 100,000 / (1 +) 1 * 2
- பிவி = $ 82,644.63 ~ $82,645
எனவே, பல்வேறு கூட்டு காலங்களுக்கான பணத்தின் தற்போதைய மதிப்பு -

பொருத்தமும் பயன்பாடும்
பணத்தின் நேர மதிப்பைப் புரிந்துகொள்வது மிகவும் முக்கியமானது, ஏனென்றால் தற்போதைய நேரத்தில் கிடைக்கும் பணம் எதிர்காலத்தில் அதன் வட்டி சம்பாதிக்கும் திறனுக்காக சமமான தொகையை விட அதிகமாக இருக்கும் என்ற கருத்தை இது கையாள்கிறது. இந்த கருத்தின் பின்னணியில் உள்ள அடிப்படை யோசனை என்னவென்றால், வட்டி சம்பாதிக்க பணத்தை முதலீடு செய்யலாம், அதே அளவு பணம் பின்னர் வந்ததை விட இன்று அதிக மதிப்புடையது.
பணத்தின் நேர மதிப்பு என்ற கருத்தை பணவீக்கம் மற்றும் வாங்கும் சக்தியின் பேச்சுவழக்கில் காணலாம். பணவீக்கம் தொடர்ந்து பணத்தின் மதிப்பை அரித்துவிடுவதால், அது இறுதியில் வாங்கும் சக்தியை எதிர்மறையாக பாதிக்கிறது. முதலீட்டின் உண்மையான வருவாயைக் கணக்கிடுவதற்காக பணவீக்கம் மற்றும் வாங்கும் திறன் இரண்டையும் இன்று முதலீடு செய்யும்போது கருத்தில் கொள்ள வேண்டும். பணவீக்க விகிதம் முதலீட்டில் எதிர்பார்க்கப்படும் வட்டி விகிதத்தை விட அதிகமாக இருந்தால், பெயரளவு வளர்ச்சி இருந்தபோதிலும், எதிர்காலத்தில் பணம் பயனற்றது, அதாவது வாங்கும் சக்தியின் அடிப்படையில் பணத்தை இழப்பது.