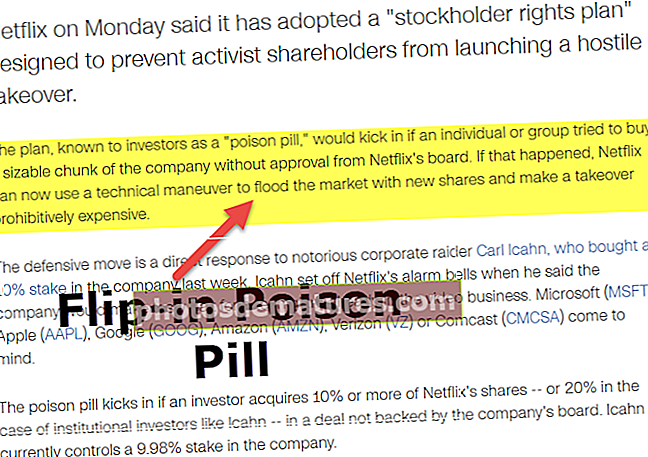
மக்கள் தொகை மாறுபாடு ஃபார்முலா | படி கணக்கீடு | எடுத்துக்காட்டுகள்
மக்கள்தொகை மாறுபாட்டைக் கணக்கிடுவதற்கான சூத்திரம்
மக்கள்தொகை மாறுபாடு சூத்திரம் என்பது மக்கள்தொகை தரவுகளின் சராசரி தூரத்தினால் அளவிடப்படுகிறது மற்றும் இது மக்கள்தொகை சூத்திரத்தின் சராசரியைக் கண்டுபிடிப்பதன் மூலம் கணக்கிடப்படுகிறது மற்றும் மாறுபாடு கணக்கிடப்படுகிறது மாறிகளின் சதுரத்தின் தொகை கழித்தல் கழித்தல் என்பது மக்கள்தொகையில் பல அவதானிப்புகளால் வகுக்கப்படுகிறது.
மக்கள்தொகை மாறுபாடு என்பது மக்கள்தொகை தரவின் பரவலின் ஒரு நடவடிக்கையாகும். எனவே, மக்கள்தொகை மாறுபாட்டை ஒரு குறிப்பிட்ட மக்கள்தொகையின் ஒவ்வொரு தரவு புள்ளியிலிருந்தும் சராசரி, சதுரத்திற்கு தூரங்களின் சராசரியாக வரையறுக்கலாம், மேலும் இது தரவு புள்ளிகள் எவ்வாறு மக்கள்தொகையில் பரவுகின்றன என்பதைக் குறிக்கிறது. மக்கள்தொகை மாறுபாடு என்பது புள்ளிவிவரங்களில் பயன்படுத்தப்படும் சிதறலின் முக்கியமான நடவடிக்கையாகும். தரவு தொகுப்பில் உள்ள தனிப்பட்ட எண்கள் ஒருவருக்கொருவர் எவ்வாறு தொடர்புபடுகின்றன என்பதை தீர்மானிக்க புள்ளிவிவர வல்லுநர்கள் மாறுபாட்டைக் கணக்கிடுகின்றனர்.
மக்கள்தொகை மாறுபாட்டைக் கணக்கிடும்போது, மக்கள்தொகை சராசரியைக் கொண்டு சிதறல் கணக்கிடப்படுகிறது. எனவே, மக்கள்தொகை மாறுபாட்டைக் கணக்கிடுவதற்கு மக்கள் தொகை அர்த்தத்தை நாம் கண்டுபிடிக்க வேண்டும். மக்கள்தொகை மாறுபாட்டின் மிகவும் பிரபலமான அறிவிப்புகளில் ஒன்று σ2 ஆகும். இது சிக்மா ஸ்கொயர் என உச்சரிக்கப்படுகிறது.
பின்வரும் சூத்திரத்தைப் பயன்படுத்தி மக்கள் தொகை மாறுபாட்டைக் கணக்கிடலாம்:


எங்கே
- σ2 என்பது மக்கள் தொகை மாறுபாடு,
- எக்ஸ்1, எக்ஸ்2, எக்ஸ்3,…..எக்ஸ்n அவதானிப்புகள்
- N என்பது அவதானிப்புகளின் எண்ணிக்கை,
- set என்பது தரவு தொகுப்பின் சராசரி
மக்கள்தொகை மாறுபாட்டின் படிப்படியான கணக்கீடு
பின்வரும் ஐந்து எளிய படிகளைப் பயன்படுத்தி மக்கள் தொகை மாறுபாட்டிற்கான சூத்திரத்தைக் கணக்கிடலாம்:
- படி 1: கொடுக்கப்பட்ட தரவின் சராசரி (µ) ஐக் கணக்கிடுங்கள். சராசரியைக் கணக்கிட, எல்லா அவதானிப்புகளையும் சேர்த்து, பின்னர் அவதானிப்புகளின் எண்ணிக்கையால் (N) வகுக்கவும்.
- படி 2: ஒரு அட்டவணையை உருவாக்கவும். அட்டவணையை உருவாக்குவது கட்டாயமில்லை என்பதை நினைவில் கொள்க, ஆனால் அதை ஒரு அட்டவணை வடிவத்தில் வழங்குவது கணக்கீடுகளை எளிதாக்கும். முதல் நெடுவரிசையில், ஒவ்வொரு அவதானிப்பையும் எழுதுங்கள் (x1, எக்ஸ்2, எக்ஸ்3,…..எக்ஸ்n).
- படி 3: இரண்டாவது நெடுவரிசையில், ஒவ்வொரு அவதானிப்பின் விலகலையும் சராசரி (x) இலிருந்து எழுதுங்கள்நான் -).
- படி 4: மூன்றாவது நெடுவரிசையில், ஒவ்வொரு அவதானிப்பின் சதுரத்தையும் சராசரி (x) இலிருந்து எழுதுங்கள்நான் - µ) 2. வேறு வார்த்தைகளில் கூறுவதானால், நெடுவரிசை 2 இல் பெறப்பட்ட ஒவ்வொரு எண்களையும் சதுரப்படுத்தவும்.
- படி 5: பின்னர் மூன்றாவது நெடுவரிசையில் பெறப்பட்ட எண்களை நாம் சேர்க்க வேண்டும். ஸ்கொயர் விலகல்களின் கூட்டுத்தொகையைக் கண்டுபிடித்து, அவதானிப்புகளின் எண்ணிக்கையால் (N) பெறப்பட்ட தொகையைப் பிரிக்கவும். இது பெற எங்களுக்கு உதவும்
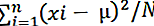 இது மக்கள் தொகை மாறுபாடு.
இது மக்கள் தொகை மாறுபாடு.
எடுத்துக்காட்டுகள்
இந்த மக்கள்தொகை மாறுபாடு ஃபார்முலா எக்செல் வார்ப்புருவை இங்கே பதிவிறக்கம் செய்யலாம் - மக்கள் தொகை மாறுபாடு ஃபார்முலா எக்செல் வார்ப்புருஎடுத்துக்காட்டு # 1
பின்வரும் 5 அவதானிப்புகளிலிருந்து மக்கள் தொகை மாறுபாட்டைக் கணக்கிடுங்கள்: 50, 55, 45, 60, 40.
தீர்வு:
மக்கள் தொகை மாறுபாட்டைக் கணக்கிடுவதற்கு பின்வரும் தரவைப் பயன்படுத்தவும்.

மொத்தம் 5 அவதானிப்புகள் உள்ளன. எனவே, என் = 5.
= (50 + 55 + 45 + 60 + 40) / 5 = 250/5 = 50
எனவே, மக்கள் தொகை மாறுபாடு σ2 இன் கணக்கீடு பின்வருமாறு செய்யப்படலாம்-


2 = 250/5
மக்கள்தொகை மாறுபாடு σ2 இருக்கும்-

மக்கள் தொகை மாறுபாடு (σ2) = 50
மக்கள் தொகை மாறுபாடு 50 ஆகும்.
எடுத்துக்காட்டு # 2
XYZ லிமிடெட் ஒரு சிறிய நிறுவனம் மற்றும் 6 ஊழியர்களை மட்டுமே கொண்டுள்ளது. இந்த ஊழியர்களின் சம்பளத்தில் அதிக சிதறல் இருக்கக்கூடாது என்று தலைமை நிர்வாக அதிகாரி நம்புகிறார். இந்த நோக்கத்திற்காக, இந்த சம்பளங்களின் மாறுபாட்டை நீங்கள் கணக்கிட வேண்டும் என்று அவர் விரும்புகிறார். இந்த ஊழியர்களின் சம்பளம் கீழ் உள்ளது. தலைமை நிர்வாக அதிகாரிக்கான சம்பளங்களின் மக்கள் தொகை மாறுபாட்டைக் கணக்கிடுங்கள்.
தீர்வு:
மக்கள் தொகை மாறுபாட்டைக் கணக்கிடுவதற்கு பின்வரும் தரவைப் பயன்படுத்தவும்.

மொத்தம் 6 அவதானிப்புகள் உள்ளன. எனவே, என் = 6.
=(30+27+20+40+32+31)/6 =180/6 =$ 30
எனவே, மக்கள் தொகை மாறுபாடு σ2 இன் கணக்கீடு பின்வருமாறு செய்யப்படலாம்-


2 = 214/6
மக்கள்தொகை மாறுபாடு σ2 இருக்கும்-

மக்கள் தொகை மாறுபாடு (σ2) = 35.67
சம்பளங்களின் மக்கள் தொகை மாறுபாடு 35.67 ஆகும்.
எடுத்துக்காட்டு # 3
ஸ்வீட் ஜூஸ் லிமிடெட் சாறுகளின் வெவ்வேறு சுவைகளை உற்பத்தி செய்கிறது. இந்த சாற்றை தொழிற்சாலையில் சேமிப்பதற்காக மேலாண்மை துறை 7 பெரிய கொள்கலன்களை வாங்குகிறது. கொள்கலன்களின் மாறுபாடு 10 க்கு மேல் இருந்தால் கொள்கலன்களை நிராகரிப்பதாக தரக் கட்டுப்பாட்டுத் துறை முடிவு செய்துள்ளது. கிலோவில் 7 கொள்கலன்களின் எடைகள் கொடுக்கப்பட்டுள்ளன: 105, 100, 102, 95, 100, 98 மற்றும் 107. தரத்திற்கு ஆலோசனை வழங்கவும் கொள்கலன்களை நிராகரிக்க வேண்டுமா என்பது குறித்து கட்டுப்பாட்டுத் துறை.
தீர்வு:
மக்கள் தொகை மாறுபாட்டைக் கணக்கிடுவதற்கு பின்வரும் தரவைப் பயன்படுத்தவும்.

மொத்தம் 7 அவதானிப்புகள் உள்ளன. எனவே, என் = 7
=(105+100+102+95+100+98+107)/7 =707/7 =10
எனவே, மக்கள் தொகை மாறுபாடு σ2 இன் கணக்கீடு பின்வருமாறு செய்யப்படலாம்-


2 = 100/7
மக்கள்தொகை மாறுபாடு σ2 இருக்கும்-

மக்கள் தொகை மாறுபாடு (σ2) = 14.29
மாறுபாடு (14.29) தரக் கட்டுப்பாட்டுத் துறையால் தீர்மானிக்கப்பட்ட 10 வரம்பை விட அதிகமாக இருப்பதால், கொள்கலன்கள் நிராகரிக்கப்பட வேண்டும்.
எடுத்துக்காட்டு # 4
சாகர் ஹெல்த்கேர் என்ற மருத்துவமனையின் நிர்வாக குழு 2019 மார்ச் முதல் வாரத்தில் 8 குழந்தைகள் பிறந்ததாக பதிவு செய்தது. குழந்தைகளின் ஆரோக்கியத்தையும் உயரங்களின் மாறுபாட்டையும் மதிப்பீடு செய்ய மருத்துவர் விரும்பினார். இந்த குழந்தைகளின் உயரங்கள் பின்வருமாறு: 48 செ.மீ, 47 செ.மீ, 50 செ.மீ, 53 செ.மீ, 50 செ.மீ, 52 செ.மீ, 51 செ.மீ, 60 செ.மீ. இந்த 8 குழந்தைகளின் உயரங்களின் மாறுபாட்டைக் கணக்கிடுங்கள்.
தீர்வு:
மக்கள் தொகை மாறுபாட்டைக் கணக்கிடுவதற்கு பின்வரும் தரவைப் பயன்படுத்தவும்.

எனவே, மக்கள் தொகை மாறுபாடு σ2 இன் கணக்கீடு பின்வருமாறு செய்யப்படலாம்-

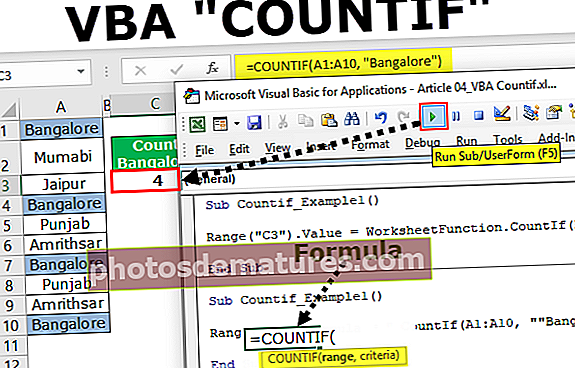
எக்செல் இல், மக்கள்தொகை மாறுபாட்டிற்கான உள்ளடிக்கிய சூத்திரம் உள்ளது, இது எண்களின் குழுவின் மக்கள்தொகை மாறுபாட்டைக் கணக்கிடப் பயன்படுகிறது. ஒரு வெற்று கலத்தைத் தேர்ந்தெடுத்து இந்த சூத்திரத்தை = VAR.P (B2: B9) எனத் தட்டச்சு செய்க. இங்கே, பி 2: பி 9 என்பது மக்கள்தொகை மாறுபாட்டைக் கணக்கிட விரும்பும் கலங்களின் வரம்பாகும்.
மக்கள்தொகை மாறுபாடு σ2 இருக்கும்-

மக்கள் தொகை மாறுபாடு (σ2) = 13.98
பொருத்தமும் பயன்பாடும்
மக்கள்தொகை மாறுபாடு சிதறலின் நடவடிக்கையாக பயன்படுத்தப்படுகிறது. ஒரே சராசரி மற்றும் அவதானிப்புகளின் எண்ணிக்கையுடன் இரண்டு மக்கள்தொகை தொகுப்புகளைக் கருத்தில் கொள்வோம். தரவு தொகுப்பு 1 5, 55, 50, 45, 50 மற்றும் 50 எண்களைக் கொண்டுள்ளது. தரவு தொகுப்பு 2 10, 50, 85, 90 மற்றும் 15 ஐக் கொண்டுள்ளது. தரவுத் தொகுப்புகள் இரண்டும் ஒரே சராசரியைக் கொண்டுள்ளன, இது 50 ஆகும். ஆனால், தரவு தொகுப்பு 1 இல், மதிப்புகள் ஒருவருக்கொருவர் நெருக்கமாக இருக்கும், தரவு தொகுப்பு 2 மதிப்புகளை சிதறடிக்கும். மாறுபாடு இந்த நெருக்கம் / சிதறலின் அறிவியல் அளவை அளிக்கிறது. டேட்டா செட் 1 இன் மாறுபாடு 10 மட்டுமே, டேட்டா செட் 2 1130 இன் பெரிய மாறுபாட்டைக் கொண்டுள்ளது. ஆகவே, ஒரு பெரிய மாறுபாடு எண்கள் சராசரி மற்றும் ஒருவருக்கொருவர் வெகு தொலைவில் இருப்பதைக் குறிக்கிறது. ஒரு சிறிய மாறுபாடு எண்கள் ஒருவருக்கொருவர் நெருக்கமாக இருப்பதைக் குறிக்கிறது.
சொத்து ஒதுக்கீட்டை மேற்கொள்ளும்போது போர்ட்ஃபோலியோ மேலாண்மை துறையில் மாறுபாடு பயன்படுத்தப்படுகிறது. வருமானம் மற்றும் நிலையற்ற தன்மை ஆகிய இரண்டு முக்கிய அளவுருக்களை மேம்படுத்துவதன் மூலம் உகந்த இலாகாக்களை தீர்மானிக்க சொத்து வருமானத்தின் மாறுபாட்டை முதலீட்டாளர்கள் கணக்கிடுகின்றனர். மாறுபாட்டால் அளவிடப்படும் ஏற்ற இறக்கம் என்பது ஒரு குறிப்பிட்ட நிதி பாதுகாப்பின் அபாயத்தின் அளவீடு ஆகும்.

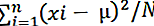 இது மக்கள் தொகை மாறுபாடு.
இது மக்கள் தொகை மாறுபாடு.