சராசரி எதிராக எடையுள்ள சராசரி | முதல் 4 வேறுபாடுகள் (இன்போ கிராபிக்ஸ் மூலம்)
சராசரி மற்றும் எடையுள்ள சராசரி என்பது எக்செல் இல் இரண்டு வெவ்வேறு சொற்கள், சராசரி என்பது கொடுக்கப்பட்ட தரவு தொகுப்பின் மைய புள்ளியைக் கணக்கிடுவதற்கான ஒரு முறையாகும், மேலும் இது எண்களைச் சேர்ப்பதற்கான சராசரியைக் கணக்கிடும் பாரம்பரிய வழியைக் கணக்கிடப்படுகிறது. சராசரியாக அதே வழியில் கணக்கிடப்படுகிறது, ஆனால் ஒவ்வொரு தரவு தொகுப்பிலும் ஒரு எடை பெருக்கப்படுகிறது.
சராசரி மற்றும் எடையுள்ள சராசரிக்கு இடையிலான வேறுபாடு
சராசரி மற்றும் எடையுள்ள சராசரி நிதி மற்றும் வணிகத்தில் கணித மற்றும் புள்ளிவிவர காலமாகும், ஆனால் இரண்டும் வித்தியாசமாக கணக்கிடப்படுகின்றன. சராசரி என்பது அனைத்து தனிப்பட்ட அவதானிப்புகளின் கூட்டுத்தொகையாகும். ஒரு குறிப்பிட்ட தரவு தொகுப்பில் நடுத்தர மதிப்பைக் கண்டுபிடிக்க அடிப்படையில் பயன்படுத்தப்படும் சராசரி. இது மையப் போக்கு என்றும் அழைக்கப்படுகிறது, மேலும் இது ஒரு குறிப்பிட்ட குழுவில் உள்ள தரவுகளின் குழுவின் மையப் போக்கைக் கண்டறியப் பயன்படுகிறது. எடையுள்ள சராசரி கணக்கியல் துறையில் பயன்படுத்தப்படுகிறது. அதன் முக்கிய நோக்கம் தீர்க்க சரியான எடை அல்லது மதிப்பைக் கண்டுபிடிப்பதாகும். எடையுள்ள சராசரி என்பது சில பத்திரங்கள் அல்லது கடன்களின் அசல் திருப்பிச் செலுத்துதலின் மதிப்பு ஆகும்.
சராசரி என்றால் என்ன?
சராசரி என்பது அனைத்து தனிப்பட்ட அவதானிப்புகளின் கூட்டுத்தொகையாகும். அடிப்படையில், இது ஒரு குறிப்பிட்ட தரவு தொகுப்பில் நடுத்தர மதிப்பைக் கண்டுபிடிக்கப் பயன்படுகிறது. இது மையப் போக்கு என்றும் அழைக்கப்படுகிறது, மேலும் இது ஒரு குறிப்பிட்ட குழுவில் உள்ள தரவுகளின் குழுவின் மையப் போக்கைக் கண்டறியப் பயன்படுகிறது. இது முக்கியமாக தரவின் பிரதிநிதித்துவத்திற்கு பயன்படுத்தப்படுகிறது. எண்கணித சூத்திரத்தைப் பயன்படுத்தி தரவுகளின் தொகுப்பிற்கு இது தீர்க்கப்படலாம்.
சராசரி சூத்திரம் = கவனித்த தொகை / அவதானிப்பின் எண்ணிக்கை
சராசரி உதாரணம்
சராசரியைப் புரிந்துகொள்ள ஒரு உதாரணத்தைப் பார்ப்போம்.
100 இல் முறையே 50, 60, 70, 80, 65, 78, 95, 63, 58, 91 மதிப்பெண்களுடன் 10 மாணவர்கள் உள்ளனர் என்று வைத்துக்கொள்வோம். இப்போது ஒரு மாணவரின் மதிப்பெண்களுக்கு சராசரியைக் கண்டுபிடிப்போம். எங்களுக்குத் தெரியும்.
சராசரி சூத்திரம் = கவனித்த தொகை / அவதானிப்பின் எண்ணிக்கை
கவனிப்பு தொகை = 50 + 60 + 70 + 80 + 65 + 78 + 95 + 63 + 58 + 9
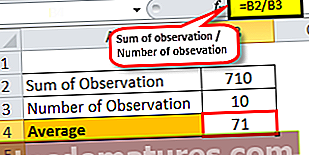
எனவே, 10 மாணவர்களின் வகுப்பின் சராசரி 71 ஆகும்.

எடையுள்ள சராசரி என்றால் என்ன?
எடையுள்ள சராசரி கணக்கியல் துறையில் பயன்படுத்தப்படுகிறது. தீர்க்க முக்கிய எடை அல்லது மதிப்பைக் கண்டுபிடிப்பதே இதன் முக்கிய நோக்கம். எடையுள்ள சராசரி என்பது சில பத்திரங்கள் அல்லது கடன்களின் அசல் திருப்பிச் செலுத்துதலின் மதிப்பு ஆகும். எடையுள்ள சராசரி என்பது சிறிய வித்தியாசத்துடன் சராசரியாக உள்ளது, ஏனெனில் எல்லா அவதானிப்புகளும் சமமான எடைகளைக் கொண்டிருக்கவில்லை, வெவ்வேறு அவதானிப்புகள் வெவ்வேறு முக்கியத்துவத்தைக் கொண்டுள்ளன, ஒவ்வொரு அவதானிப்பும் எடையால் பெருக்கப்பட்டு சேர்க்கப்படுகின்றன. எடை சராசரி செய்ய பயன்படுத்தப்படுகிறது. ஒவ்வொரு மதிப்பும் வெவ்வேறு எடையைக் கொண்ட சராசரியாக இதை எடுத்துக் கொள்ளலாம். இது தரவு மதிப்பின் எடையால் பாதிக்கப்படுகிறது. எடையுள்ள மதிப்பு என்பது எடையின் எண்ணிக்கையால் வகுக்கப்பட்டுள்ள எடையுள்ள அவதானிப்பின் உற்பத்தியின் கூட்டுத்தொகை மற்றும் இதை எழுதலாம்: -
எடையுள்ள சராசரி ஃபார்முலா = (a1w1 + a2w2 + a3w3 +… + anwn) / (w1 + w2 + w3… + wn)
எடையுள்ள சராசரிக்கு எடுத்துக்காட்டு
அதை நன்றாக புரிந்துகொள்ள ஒரு உதாரணத்தைப் பார்ப்போம்.
ஒரு வருடத்திற்கு இறுதி மதிப்பெண்கள் வழங்க பங்களிக்கும் மூன்று வெவ்வேறு தேர்வுகள் உள்ளன என்று வைத்துக்கொள்வோம், முதல் பரீட்சை எடைக்கு ஒவ்வொரு தேர்வின் வெவ்வேறு எடை 15%, இரண்டாவது தேர்வு எடை 25% மற்றும் இறுதி தேர்வு எடை 60% என இப்போது அனுமானிக்கலாம் ஒரு மாணவர் முதல் தேர்வில் 60 மதிப்பெண்களையும், இரண்டாவது தேர்வில் 70 புள்ளிகளையும், இறுதித் தேர்வில் 100 மதிப்பெண்களில் 80 மதிப்பெண்களையும் பெற்றுள்ளார், இப்போது ஒரு மாணவரின் இறுதி மதிப்பெண்களைக் கணக்கிடுவோம்.
அதன் கணக்கீட்டிற்கு மேலே குறிப்பிட்ட சூத்திரத்தைப் பயன்படுத்தவும்.
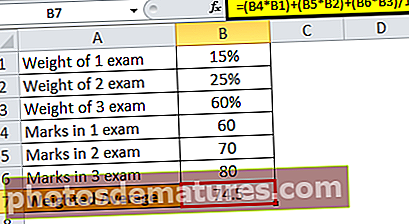
- எனவே, ஒரு மாணவரின் சராசரி சராசரி 74.5 ஆகும்.
சராசரி vs எடையுள்ள சராசரி இன்போ கிராபிக்ஸ்
இங்கே நாங்கள் உங்களுக்கு முதல் 5 வேறுபாடுகளை வழங்குகிறோம்.
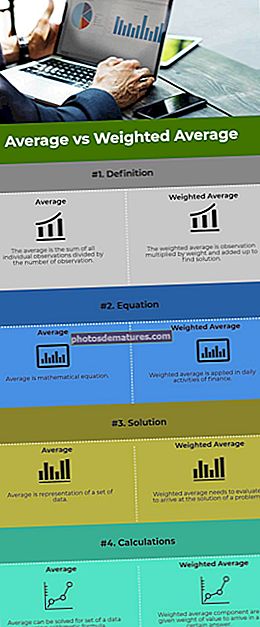
சராசரி vs எடையுள்ள சராசரி - முக்கிய வேறுபாடுகள்
இந்த சராசரிக்கு இடையிலான முக்கிய வேறுபாடுகள் பின்வருமாறு -
- சராசரி என்பது அனைத்து தனிப்பட்ட அவதானிப்புகளின் கூட்டுத்தொகையாகும், அதேசமயம் எடையுள்ள சராசரி என்பது எடையால் பெருக்கப்பட்டு ஒரு தீர்வைக் காண சேர்க்கப்படுகிறது.
- சராசரி என்பது ஒரு கணித சமன்பாடாகும், அதே சமயம் எடையுள்ள சராசரி நிதியத்தின் அன்றாட நடவடிக்கைகளில் பயன்படுத்தப்படுகிறது.
- சராசரி என்பது தரவுகளின் தொகுப்பின் பிரதிநிதித்துவமாகும், அதேசமயம் எடையுள்ள சராசரி ஒரு பிரச்சினையின் தீர்வைப் பெறுவதற்கு மதிப்பீடு செய்ய வேண்டும்.
- எண்கணித சூத்திரத்தைப் பயன்படுத்தி தரவுகளின் தொகுப்பிற்கு சராசரியாக தீர்க்க முடியும் மற்றும் எடையுள்ள சராசரி கூறுக்கு ஒரு குறிப்பிட்ட பதிலில் வருவதற்கு மதிப்பின் எடை வழங்கப்படுகிறது.
சராசரி vs எடையுள்ள சராசரி தலை முதல் தலை வேறுபாடு
இப்போது தலையில் இருந்து வேறுபாடுகளைப் பார்ப்போம்.
| அடிப்படை | சராசரி | எடை சராசரி | ||
| வரையறை | இது அனைத்து தனிப்பட்ட அவதானிப்புகளின் கூட்டுத்தொகையாகும். | இது எடையால் பெருக்கப்பட்டு ஒரு தீர்வைக் காண சேர்க்கப்படுகிறது. | ||
| சமன்பாடு | இது ஒரு கணித சமன்பாடு. | இது நிதியத்தின் அன்றாட நடவடிக்கைகளில் பயன்படுத்தப்படுகிறது. | ||
| தீர்வு | இது தரவுகளின் தொகுப்பின் பிரதிநிதித்துவம் ஆகும். | ஒரு பிரச்சினையின் தீர்வைப் பெறுவதற்கு இது மதிப்பீடு செய்ய வேண்டும். | ||
| கணக்கீடுகள் | எண்கணித சூத்திரத்தைப் பயன்படுத்தி தரவுகளின் தொகுப்பிற்கு இது தீர்க்கப்படலாம். | கூறு ஒரு குறிப்பிட்ட பதிலில் வருவதற்கு மதிப்பின் எடை வழங்கப்படுகிறது. |
முடிவுரை
எனவே, சராசரி vs வெயிட்டட் சராசரியைக் கண்டோம், இரண்டிற்கும் இடையிலான வித்தியாசத்தைக் கண்டோம். சராசரி என்பது அவதானிப்பின் எண்ணிக்கையால் வகுக்கப்பட்டுள்ள அனைத்து தனிப்பட்ட அவதானிப்புகளின் கூட்டுத்தொகையாகும், எண்கணித சூத்திரத்தைப் பயன்படுத்துவதன் மூலம் ஒரு தரவுகளின் தொகுப்பிற்கு சராசரியாக தீர்க்க முடியும், அதே சமயம் எடையுள்ள சராசரி என்பது ஒரு எடையால் பெருக்கப்பட்டு ஒரு கண்டுபிடிப்பைக் கூட்டும் தீர்வு மற்றும் எடையுள்ள சராசரி கூறு ஒரு குறிப்பிட்ட பதிலில் வருவதற்கு மதிப்பின் எடை வழங்கப்படுகிறது. இருவரும் பிரச்சினையின் அடிப்படையில் வெவ்வேறு பயனர்களைக் கொண்டுள்ளனர் மற்றும் இருவரும் வித்தியாசமாக கணக்கிடப்படுகிறார்கள். எடையுள்ள சராசரியின் முக்கிய நோக்கம் சரியான எடை அல்லது தீர்க்க மதிப்பைக் கண்டுபிடிப்பதாகும். ஒரு சராசரி மதிப்பு செலுத்தப்படும் வரை சில பத்திரங்கள் அல்லது கடன்களின் அசல் திருப்பிச் செலுத்துதலின் சராசரி மதிப்பு எடையுள்ள சராசரி. சராசரி மதிப்பு அல்லது சராசரி மதிப்பைக் கண்டுபிடிக்க சராசரி பயன்படுத்தப்படுகிறது.