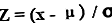இசட் ஸ்கோர் ஃபார்முலா | இசட்-ஸ்கோரின் படி கணக்கீடு
இசட்-ஸ்கோரைக் கணக்கிட ஃபார்முலா
மூல தரவுகளின் இசட் மதிப்பெண் என்பது மக்கள்தொகைக்கு மேலே அல்லது அதற்குக் கீழே எத்தனை நிலையான விலகல்களை அளவிடுவதன் மூலம் உருவாக்கப்படும் மதிப்பெண்ணைக் குறிக்கிறது, இது பரிசீலனையில் உள்ள கருதுகோளை சோதிக்க உதவுகிறது. வேறு வார்த்தைகளில் கூறுவதானால், இது மக்களிடமிருந்து ஒரு தரவு புள்ளியின் தூரம் என்பது நிலையான விலகலின் பலமாக வெளிப்படுத்தப்படுகிறது.
- Z- மதிப்பெண்கள் நிலையான விலகல் -3 மடங்கு (சாதாரண விநியோகத்தின் இடதுபுறம்) +3 மடங்கு நிலையான விலகலில் (சாதாரண விநியோகத்தின் வலது வலது) மாறுபடும்.
- Z- மதிப்பெண்கள் 0 இன் சராசரி மற்றும் 1 இன் நிலையான விலகலைக் கொண்டுள்ளன.
தரவு புள்ளியின் z- மதிப்பெண்ணின் சமன்பாடு தரவு புள்ளியிலிருந்து மக்கள்தொகை சராசரியைக் கழிப்பதன் மூலம் கணக்கிடப்படுகிறது (என குறிப்பிடப்படுகிறது எக்ஸ்) பின்னர் முடிவு மக்கள் தொகை விலகலால் வகுக்கப்படுகிறது. கணித ரீதியாக, இது,
இசட் ஸ்கோர் = (x - μ) / ø
எங்கே
- x = டேட்டாபாயிண்ட்
- μ = சராசரி
- Standard = நிலையான விலகல்
இசட் மதிப்பெண் கணக்கீடு (படிப்படியாக)
தரவு புள்ளியின் z- மதிப்பெண்ணிற்கான சமன்பாடு பின்வரும் படிகளைப் பயன்படுத்தி பெறலாம்:
- படி 1: முதலாவதாக, x ஆல் குறிக்கப்படும் தரவு புள்ளிகள் அல்லது அவதானிப்புகளின் அடிப்படையில் தரவு தொகுப்பின் சராசரியை தீர்மானிக்கவும்நான், தரவு தொகுப்பில் உள்ள மொத்த தரவு புள்ளிகளின் எண்ணிக்கை N. ஆல் குறிக்கப்படுகிறது.

- படி 2: அடுத்து, மக்கள்தொகையின் அடிப்படையில் மக்கள்தொகையின் நிலையான விலகலை தீர்மானிக்கவும் mean, தரவு புள்ளிகள் xநான் மற்றும் மக்கள்தொகையில் தரவு புள்ளிகளின் எண்ணிக்கை N.

- படி 3: இறுதியாக, z- மதிப்பெண் தரவு புள்ளியிலிருந்து சராசரியைக் கழிப்பதன் மூலம் பெறப்படுகிறது, பின்னர் இதன் விளைவாக கீழே காட்டப்பட்டுள்ளபடி நிலையான விலகலால் வகுக்கப்படுகிறது.
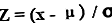
எடுத்துக்காட்டுகள்
இந்த இசட் ஸ்கோர் ஃபார்முலா எக்செல் வார்ப்புருவை இங்கே பதிவிறக்கம் செய்யலாம் - இசட் ஸ்கோர் ஃபார்முலா எக்செல் வார்ப்புருஎடுத்துக்காட்டு # 1
கடந்த வாரம் அறிவியல் தேர்வை எழுதிய 50 மாணவர்களின் வகுப்பின் உதாரணத்தை எடுத்துக் கொள்வோம். இன்று முடிவு நாள் மற்றும் வகுப்பு ஆசிரியர் ஜான் தேர்வில் 93 மதிப்பெண்களைப் பெற்றார், வகுப்பின் சராசரி மதிப்பெண் 68 ஆக இருந்தது என்று கூறினார். நிலையான விலகல் 13 ஆக இருந்தால் ஜானின் சோதனை அடையாளத்திற்கான z- மதிப்பெண்ணைத் தீர்மானிக்கவும்.
தீர்வு:
கொடுக்கப்பட்ட,
- ஜானின் சோதனை மதிப்பெண், x = 93
- சராசரி, μ = 68
- நிலையான விலகல், ơ = 13

ஆகையால், ஜானின் சோதனை மதிப்பெண்ணிற்கான z- மதிப்பெண்ணை மேற்கண்ட சூத்திரத்தைப் பயன்படுத்தி கணக்கிடலாம்,

இசட் = (93 - 68) / 13
இசட் ஸ்கோர் இருக்கும் -

இசட் ஸ்கோர் = 1.92
ஆகையால், ஜானின் Ztest மதிப்பெண் என்பது வகுப்பின் சராசரி மதிப்பெண்ணை விட 1.92 நிலையான விலகலாகும், அதாவது வகுப்பில் 97.26% (49 மாணவர்கள்) ஜானை விட குறைவாக மதிப்பெண் பெற்றனர்.
எடுத்துக்காட்டு # 2
வகுப்புத் தேர்வுக்குத் தோன்றிய 30 மாணவர்களின் (30-க்கும் குறைவான தரவு புள்ளிகளுக்கு z- சோதனை பொருத்தமானதல்ல) மற்றொரு விரிவான உதாரணத்தை எடுத்துக்கொள்வோம். 100 - 55, 67, 84, 65, 59, 68, 77, 95, 88, 78, 53, 81, 73, 66 இல் மாணவர்கள் பெற்ற மதிப்பெண்களின் அடிப்படையில் 4 வது மாணவருக்கான z- சோதனை மதிப்பெண்ணை தீர்மானிக்கவும். , 65, 52, 54, 83, 86, 94, 85, 72, 62, 64, 74, 82, 58, 57, 51, 91.
தீர்வு:
கொடுக்கப்பட்ட,
- x = 65,
- 4 வது மாணவர் மதிப்பெண் = 65,
- தரவு புள்ளிகளின் எண்ணிக்கை, N = 30.
சராசரி = (55 + 67 + 84 + 65 + 59 + 68 + 77 + 95 + 88 + 78 + 53 + 81 + 73 + 66 + 65 + 52 + 54 + 83 + 86 + 94 + 85 + 72 + 62 + 64 + 74 + 82 + 58 + 57 + 51 + 91) / 30
சராசரி = 71.30
இப்போது, கீழே காட்டப்பட்டுள்ளபடி சூத்திரத்தைப் பயன்படுத்தி நிலையான விலகலைக் கணக்கிட முடியும்,

= 13.44
எனவே, 4 வது மாணவரின் இசட் மதிப்பெண்ணை மேற்கண்ட சூத்திரத்தைப் பயன்படுத்தி கணக்கிடலாம்,
Z = (x - x) / s
- இசட் = (65 –30) / 13.44
- இசட் = -0.47
ஆகையால், 4 வது மாணவரின் மதிப்பெண் வகுப்பின் சராசரி மதிப்பெண்ணை விட 0.47 நிலையான விலகலாகும், அதாவது வகுப்பில் 31.92% (10 மாணவர்கள்) 4-வது மாணவரை விட z- மதிப்பெண் அட்டவணையின்படி குறைவாக மதிப்பெண் பெற்றனர்.
எக்செல் இல் Z மதிப்பெண் (எக்செல் வார்ப்புருவுடன்)
இப்போது, கீழேயுள்ள எக்செல் வார்ப்புருவில் z- மதிப்பெண் கருத்தை விளக்குவதற்கு எடுத்துக்காட்டு 2 இல் குறிப்பிடப்பட்டுள்ள வழக்கை எடுத்துக் கொள்வோம்.
இசட் மதிப்பெண்ணைக் கணக்கிடுவதற்கான தரவு கீழே கொடுக்கப்பட்டுள்ளது


இசட் ஸ்கோர் ஃபார்முலா டெஸ்ட் புள்ளிவிவரங்களின் விரிவான கணக்கீட்டிற்கு கீழே கொடுக்கப்பட்டுள்ள எக்செல் தாளை நீங்கள் பார்க்கலாம்.
சம்பந்தம் மற்றும் பயன்கள்
கருதுகோள் சோதனையின் கண்ணோட்டத்தில், z- மதிப்பெண் புரிந்து கொள்ள ஒரு மிக முக்கியமான கருத்தாகும், ஏனெனில் ஒரு சோதனை புள்ளிவிவரம் ஏற்றுக்கொள்ளத்தக்க மதிப்பின் வரம்பில் வருகிறதா இல்லையா என்பதை சோதிக்க இது பயன்படுத்தப்படுகிறது. பகுப்பாய்விற்கு முன்னர் தரவை தரப்படுத்தவும், மதிப்பெண்ணின் நிகழ்தகவைக் கணக்கிடவும் அல்லது வெவ்வேறு சாதாரண விநியோகங்களிலிருந்து வரும் இரண்டு அல்லது அதற்கு மேற்பட்ட தரவு புள்ளிகளின் ஒப்பீட்டையும் z- மதிப்பெண் பயன்படுத்தப்படுகிறது. ஒழுங்காகப் பயன்படுத்தினால் புலங்களில் z- மதிப்பெண்ணின் மாறுபட்ட பயன்பாடு உள்ளது.