வருடாந்திர ஃபார்முலாவின் தற்போதைய மதிப்பு | வருடாந்திரத்தின் பி.வி கணக்கிடவா? | எடுத்துக்காட்டுகள்
வருடாந்திரத்தின் பி.வி.யைக் கணக்கிடுவதற்கான சூத்திரம்
வருடாந்திர சூத்திரத்தின் தற்போதைய மதிப்பு ஒரு பிளஸ் தள்ளுபடி வீதத்தால் வகுக்கப்பட்ட காலப்பகுதியில் வருடாந்திர கொடுப்பனவுகளால் கணக்கிடப்படும் தற்போதைய மதிப்பை நிர்ணயிப்பதன் மூலம் கணக்கிடப்படுகிறது மற்றும் வருடாந்திரத்தின் தற்போதைய மதிப்பு சமமான மாதாந்திர கொடுப்பனவுகளை ஒரு கழித்தல் தற்போதைய மதிப்பால் தள்ளுபடி செய்வதன் மூலம் வகுக்கப்படுகிறது. வீதம்.
வருடாந்திரத்தின் பி.வி = சி x [(1 - (1 + i) -n) / i]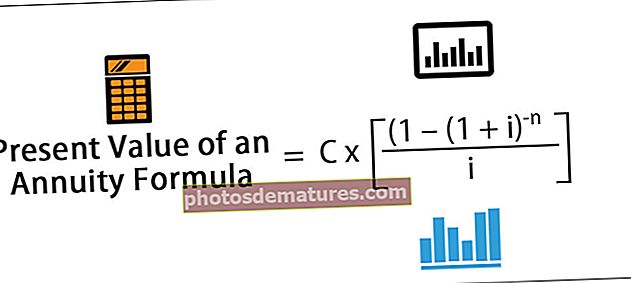
எங்கே,
- சி என்பது ஒரு காலத்திற்கு பணப்புழக்கம்
- நான் வட்டி விகிதம்
- n என்பது கொடுப்பனவுகளின் அதிர்வெண்
விளக்கம்
பி.வி. சூத்திரம் ஒரு குறிப்பிட்ட காலகட்டத்தில் தீர்மானிக்கும், இது பல எதிர்கால சரியான நேர இடைவெளிக் கொடுப்பனவுகளின் தற்போதைய மதிப்பு. வருடாந்திர சூத்திரத்தின் பி.வி., இது பணக் கருத்தின் நேர மதிப்பைப் பொறுத்தது என்ற சூத்திரத்திலிருந்து காணலாம், இதில் நடப்பு நாளில் ஒரு டாலர் பணம் அதே டாலரை விட மிகவும் தகுதியானது, இது ஒரு தேதியில் வரவுள்ளது எதிர்காலத்தில் நடக்கப்போகிறது. மேலும், வருடாந்திர சூத்திரத்தின் பி.வி கட்டணம் வருடாந்திர, அரை ஆண்டு, மாதாந்திரம் போன்றவற்றைக் கவனித்துக்கொள்கிறது, அதன்படி கணக்கீடு செய்கிறது அல்லது கூட்டுகிறது என்று கூறுகிறது.
எடுத்துக்காட்டுகள்
வருடாந்திர ஃபார்முலா எக்செல் வார்ப்புருவின் தற்போதைய மதிப்பை இங்கே பதிவிறக்கம் செய்யலாம் - வருடாந்திர ஃபார்முலா எக்செல் வார்ப்புருவின் தற்போதைய மதிப்புஎடுத்துக்காட்டு # 1
ஆண்டின் ஒவ்வொரு முடிவிலும் தொடங்கி அடுத்த 25 ஆண்டுகளுக்கு $ 1,000 வருடாந்திர கட்டணம் செலுத்தப்படுகிறது என்று வைத்துக்கொள்வோம். வருடாந்திரத்தின் தற்போதைய மதிப்பை நீங்கள் கணக்கிட வேண்டும், வட்டி விகிதம் 5% என்று கருதி.
தீர்வு:
இங்கே வருடாந்திரங்கள் ஆண்டின் இறுதியில் தொடங்குகின்றன, எனவே n 25 ஆக இருக்கும், அடுத்த 25 ஆண்டுகளுக்கு C $ 1,000 மற்றும் நான் 5%.
வருடாந்திரத்தின் பி.வி கணக்கிட பின்வரும் தரவைப் பயன்படுத்தவும்.

எனவே, வருடாந்திரத்தின் பி.வி.யின் கணக்கீட்டை பின்வருமாறு செய்யலாம் -

வருடாந்திரத்தின் தற்போதைய மதிப்பு -

= $ 1,000 x [(1 - (1 + 5%) - 25) / 0.05]
வருடாந்திரத்தின் தற்போதைய மதிப்பு = 14,093.94
எடுத்துக்காட்டு # 2
ஜெஓன் தற்போது ஒரு எம்.என்.சி.யில் பணிபுரிகிறார், அங்கு அவருக்கு ஆண்டுக்கு $ 10,000 வழங்கப்படுகிறது. அவரது இழப்பீட்டில், 25% பகுதி உள்ளது, இது நிறுவனத்தால் வருடாந்திரமாக செலுத்தப்படும். இந்த பணம் ஒரு வருடத்தில் இரண்டு முறை டெபாசிட் செய்யப்படுகிறது, ஜூலை 1 ஆம் தேதி தொடங்கி இரண்டாவது ஜனவரி 1 ஆம் தேதி வரவுள்ளது, அடுத்த 30 ஆண்டுகள் வரை தொடரும் மற்றும் மீட்பின் போது, அது வரிவிலக்கு அளிக்கப்படும்.
ஒரே நேரத்தில், 000 60,000 எடுக்க சேர அவருக்கு ஒரு விருப்பமும் வழங்கப்பட்டது, ஆனால் அது 40% என்ற விகிதத்தில் வரிக்கு உட்பட்டது. ஜான் இப்போது பணத்தை எடுக்க வேண்டுமா அல்லது 30 ஆண்டுகள் வரை காத்திருக்க வேண்டுமா என்பதை நீங்கள் மதிப்பிட வேண்டும், அதேபோல் அவர் நிதி தேவை இல்லை என்றும் சந்தையில் ஆபத்து இல்லாத விகிதம் 6% என்றும் கருதுகிறார்.
தீர்வு
இங்கே, வருடாந்திரங்கள் அரை ஆண்டு முடிவில் தொடங்குகின்றன, எனவே n 60 (30 * 2) ஆக இருக்கும், சி அடுத்த 30 ஆண்டுகளுக்கு $ 1,250 ($ 10,000 * 25% / 2) மற்றும் நான் 2.5% (5% / 2) ).
வருடாந்திரத்தின் தற்போதைய மதிப்பைக் கணக்கிட பின்வரும் தரவைப் பயன்படுத்தவும்.

எனவே, வருடாந்திர சூத்திரத்தின் (பி.வி) தற்போதைய மதிப்பைக் கணக்கிடுவது பின்வருமாறு செய்யப்படலாம் -

வருடாந்திரத்தின் தற்போதைய மதிப்பு -

= $ 1,250 x [(1 - (1 + 2.5%) - 60) / 0.025]
வருடாந்திரத்தின் தற்போதைய மதிப்பு = $ 38,635.82
எனவே, ஜான் வருடாந்திரத்தைத் தேர்வுசெய்தால், அவர், 6 38,635.82 பெறுவார்.
இரண்டாவது விருப்பம் அவர் வரிக்கு முந்தைய $ 60,000 ஐத் தேர்வுசெய்கிறார், நாங்கள் 40% வரியைக் கழித்தால் கையில் உள்ள தொகை, 000 36,000 ஆகும்.
எனவே, 6 2,635.82 க்கு ஒரு நன்மை இருப்பதால் ஜான் வருடாந்திரத்தைத் தேர்வு செய்ய வேண்டும்
எடுத்துக்காட்டு # 3
திருமதி கார்மெல்லா ஓய்வு பெறுவதற்கு அருகில் இருப்பதால் இரண்டு வெவ்வேறு ஓய்வூதிய தயாரிப்புகள் வழங்கப்படுகின்றன. இரண்டு தயாரிப்புகளும் 60 வயதில் தங்கள் பணப்புழக்கத்தைத் தொடங்கி 80 வயது வரை வருடாந்திரத்தைத் தொடரும். தயாரிப்புகளின் கூடுதல் விவரங்கள் கீழே. வருடாந்திரத்தின் தற்போதைய மதிப்பை நீங்கள் கணக்கிட வேண்டும் மற்றும் திருமதி கார்மெல்லாவுக்கு சிறந்த தயாரிப்பு எது என்று ஆலோசனை கூற வேண்டும்?
வட்டி விகிதம் 7% என்று வைத்துக் கொள்ளுங்கள்.
1) தயாரிப்பு எக்ஸ்
வருடாந்திர தொகை = ஒரு காலத்திற்கு, 500 2,500. கொடுப்பனவு அதிர்வெண் = காலாண்டு. கட்டணம் காலத்தின் தொடக்கத்தில் இருக்கும்
2) தயாரிப்பு ஒய்
வருடாந்திர தொகை = ஒரு காலத்திற்கு 5,150. கொடுப்பனவு அதிர்வெண் = அரை ஆண்டு. கட்டணம் காலத்தின் முடிவில் இருக்கும்
கொடுக்கப்பட்ட,

தீர்வு:
இங்கே, தயாரிப்பு x க்கான வருடாந்திரங்கள் காலாண்டின் தொடக்கத்தில் தொடங்குகிறது, எனவே வருடாந்திரத்தின் தொடக்கத்தில் பணம் செலுத்தப்படுவதால் n 79 ஆக இருக்கும் (20 * 4 குறைவாக 1), சி அடுத்த 20 ஆண்டுகளுக்கு, 500 2,500 மற்றும் நான் 1.75% (7% / 4).
எனவே, ஒரு தயாரிப்பு X க்கான வருடாந்திரத்தின் தற்போதைய மதிப்பைக் கணக்கிடுவது பின்வருமாறு செய்யப்படலாம் -

வருடாந்திரத்தின் தற்போதைய மதிப்பு தயாரிப்பு எக்ஸ் இருக்கும் -

= $ 2,500 x [(1 - (1 + 1.75%) - 79) / 0.0175]
வருடாந்திரத்தின் தற்போதைய மதிப்பு = $ 106,575.83
இந்த காலத்தின் தொடக்கத்தில் பெறப்பட்டதிலிருந்து இப்போது நாம் value 2,500 ஐ தற்போதைய மதிப்புக்கு மேல் சேர்க்க வேண்டும், எனவே மொத்த தொகை 1,09,075.83 ஆக இருக்கும்
2 வது விருப்பம் அரை ஆண்டுதோறும் செலுத்துகிறது, எனவே n 40 (20 * 2), நான் 3.50% (7% / 2) மற்றும் சி $ 5,150 ஆக இருக்கும்.
எனவே, ஒரு தயாரிப்பு Y க்கான வருடாந்திரத்தின் பி.வி கணக்கீடு பின்வருமாறு செய்யப்படலாம் -

தயாரிப்பு Y க்கான வருடாந்திரத்தின் தற்போதைய மதிப்பு -

= $ 5,150 x [(1 - (1 + 3.50%) - 40) / 0.035]
வருடாந்திரத்தின் தற்போதைய மதிப்பு = 9 109,978.62
விருப்பம் 2 ஐத் தேர்ந்தெடுக்கும்போது 2 902.79 அதிகமாக மட்டுமே உள்ளது, எனவே திருமதி கார்மெல்லா விருப்பம் 2 ஐத் தேர்ந்தெடுக்க வேண்டும்.
சம்பந்தம் மற்றும் பயன்கள்
ஓய்வூதிய விருப்பங்களை கணக்கிடுவதில் மட்டுமல்லாமல் சூத்திரம் மிகவும் முக்கியமானது, ஆனால் இது மூலதன பட்ஜெட்டின் விஷயத்தில் பணப்பரிமாற்றத்திற்கும் பயன்படுத்தப்படலாம், இங்கு வாடகை அல்லது குறிப்பிட்ட கால வட்டி செலுத்தப்பட்டதற்கு ஒரு எடுத்துக்காட்டு இருக்கக்கூடும், அவை பெரும்பாலும் நிலையானவை, எனவே அவை தள்ளுபடி செய்யப்படலாம் இந்த வருடாந்திர சூத்திரத்தைப் பயன்படுத்துகிறது. மேலும், சூத்திரத்தைப் பயன்படுத்தும் போது ஒருவர் எச்சரிக்கையாக இருக்க வேண்டும், ஏனெனில் காலத்தின் தொடக்கத்திலோ அல்லது காலத்தின் முடிவிலோ பணம் செலுத்தப்படுகிறதா என்பதை தீர்மானிக்க வேண்டும், அதேபோல் கூட்டு விளைவுகள் காரணமாக பணப்புழக்கங்களின் மதிப்புகளை பாதிக்கலாம்.