கால சூத்திரம் (வரையறை, எக்செல் எடுத்துக்காட்டுகள்) | பாண்டின் கால அளவைக் கணக்கிடுங்கள்
கால ஃபார்முலா என்றால் என்ன?
காலத்திற்கான சூத்திரம் என்பது வட்டி விகிதத்தில் ஏற்படும் மாற்றங்களுக்கான ஒரு பத்திரத்தின் உணர்திறன் அளவீடு ஆகும், மேலும் இது பத்திரத்தின் தள்ளுபடி செய்யப்பட்ட எதிர்கால பண வரவின் மொத்த உற்பத்தியையும், அதனுடன் தொடர்புடைய ஆண்டுகளையும் தள்ளுபடி செய்யப்பட்ட எதிர்கால பண வரவின் தொகையால் வகுப்பதன் மூலம் கணக்கிடப்படுகிறது. பணப்புழக்கம் அடிப்படையில் கூப்பன் கட்டணம் மற்றும் முடிவில் முதிர்வு ஆகியவற்றைக் கொண்டுள்ளது. இது மக்காலே காலம் என்றும் அழைக்கப்படுகிறது.
கணித ரீதியாக, காலத்திற்கான சமன்பாடு கீழே குறிப்பிடப்படுகிறது,

எங்கே,
- சி = ஒரு காலத்திற்கு கூப்பன் கட்டணம்
- எம் = முகம் அல்லது சம மதிப்பு
- r = பயனுள்ள கால வட்டி விகிதம்
- n = முதிர்ச்சிக்கான காலங்களின் எண்ணிக்கை
மேலும், பத்திரத்தின் தள்ளுபடி செய்யப்பட்ட பணப்புழக்கத்தின் கூட்டுத்தொகையாகும், இது பத்திரத்தின் தற்போதைய மதிப்பு அல்லது விலைக்கு சமமாகும். எனவே, காலத்திற்கான சூத்திரத்தை மேலும் கீழே எளிமைப்படுத்தலாம்,

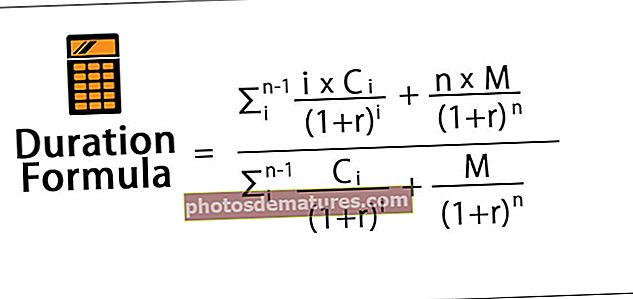
கால சூத்திரத்தின் விளக்கம்
காலத்திற்கான சமன்பாட்டை பின்வரும் படிகளைப் பயன்படுத்தி கணக்கிடலாம்:
படி 1: முதலாவதாக, பத்திர வெளியீட்டின் முகம் அல்லது சம மதிப்பு கண்டுபிடிக்கப்பட்டது மற்றும் அது எம்.
படி 2: இப்போது, பத்திரத்தின் கூப்பன் கட்டணம் வட்டி பயனுள்ள கால விகிதத்தின் அடிப்படையில் கணக்கிடப்படுகிறது. பின்னர் கூப்பன் கட்டணத்தின் அதிர்வெண்ணும் தீர்மானிக்கப்படுகிறது. கூப்பன் கொடுப்பனவு C ஆல் குறிக்கப்படுகிறது மற்றும் பயனுள்ள வட்டி விகிதம் r ஆல் குறிக்கப்படுகிறது.
படி 3: இப்போது, முதிர்வு வரை மொத்த காலங்களின் எண்ணிக்கை முதிர்வு வரை ஆண்டுகளின் எண்ணிக்கையையும் ஒரு வருடத்தில் கூப்பன் கொடுப்பனவுகளின் அதிர்வெண்ணையும் பெருக்கி கணக்கிடப்படுகிறது. முதிர்வு வரை காலங்களின் எண்ணிக்கை n ஆல் குறிக்கப்படுகிறது. மேலும், அவ்வப்போது செலுத்தும் நேரம் குறிப்பிடப்பட்டுள்ளது, இது i ஆல் குறிக்கப்படுகிறது.
படி 4: இறுதியாக, கிடைக்கக்கூடிய தகவல்களின் அடிப்படையில் காலத்திற்கான சமன்பாட்டை கீழே காணலாம்,

கால ஃபார்முலாவின் எடுத்துக்காட்டுகள் (எக்செல் வார்ப்புருவுடன்)
இதை நன்கு புரிந்துகொள்ள சில எளிய மற்றும் மேம்பட்ட கால அளவு சூத்திரத்தைப் பார்ப்போம்.
இந்த கால ஃபார்முலா எக்செல் வார்ப்புருவை இங்கே பதிவிறக்கம் செய்யலாம் - கால ஃபார்முலா எக்செல் வார்ப்புரு
கால ஃபார்முலா ஃபார்முலா - எடுத்துக்காட்டு # 1
வருடாந்திர கூப்பன் கொடுப்பனவுகளுடன் ஒரு பத்திரத்தின் உதாரணத்தை எடுத்துக்கொள்வோம். XYZ லிமிடெட் நிறுவனம், 000 100,000 முக மதிப்பைக் கொண்ட ஒரு பத்திரத்தை ஆண்டு கூப்பன் வீதத்தை 7% சுமந்து 5 ஆண்டுகளில் முதிர்ச்சியடையச் செய்துள்ளது என்று வைத்துக் கொள்வோம். நடைமுறையில் உள்ள சந்தை வட்டி விகிதம் 10% ஆகும்.
கொடுக்கப்பட்ட, எம் = $ 100,000
- சி = 7% * $ 100,000 = $ 7,000
- n = 5
- r = 10%
வகுத்தல் அல்லது பத்திரத்தின் விலை சூத்திரத்தைப் பயன்படுத்தி கணக்கிடப்படுகிறது,

- பத்திர விலை = 84,281.19
கால சூத்திரத்தின் எண்ணிக்கையின் கணக்கீடு பின்வருமாறு -

= (6,363.64 + 11,570.25 + 15,777.61 + 19,124.38 + 310,460.70)
= 363,296.50
எனவே, பத்திரத்தின் கால அளவீடு கீழே இருக்கும்,

காலம் = 363,296.50 / 84,281.19
- காலம் = 4.31 ஆண்டுகள்
கால ஃபார்முலா ஃபார்முலா - எடுத்துக்காட்டு # 2
வருடாந்திர கூப்பன் கொடுப்பனவுகளுடன் ஒரு பத்திரத்தின் உதாரணத்தை எடுத்துக்கொள்வோம். XYZ லிமிடெட் நிறுவனம், 000 100,000 முக மதிப்பு மற்றும் 4 ஆண்டுகளில் முதிர்ச்சியடைந்த ஒரு பத்திரத்தை வெளியிட்டுள்ளது என்று வைத்துக் கொள்வோம். நடைமுறையில் உள்ள சந்தை வட்டி விகிதம் 10% ஆகும். பின்வரும் வருடாந்திர கூப்பன் வீதத்திற்கான பத்திர கால அளவைக் கணக்கிடுங்கள்: (அ) 8% (பி) 6% (சி) 4%
கொடுக்கப்பட்ட, எம் = $ 100,000
- n = 4
- r = 10%
கூப்பன் வீதத்திற்கான கணக்கீடு 8%
கூப்பன் கட்டணம் (சி) = 8% * $ 100,000 = $ 8,000
வகுத்தல் அல்லது பத்திரத்தின் விலை சூத்திரத்தைப் பயன்படுத்தி கணக்கிடப்படுகிறது,

- பத்திர விலை = 88,196.16
கால சூத்திரத்தின் எண்ணிக்கையின் கணக்கீடு பின்வருமாறு இருக்கும் -

= 311,732.8
எனவே, பத்திரத்தின் கால அளவீடு கீழே இருக்கும்,

காலம் = 311,732.81 / 88,196.16
- காலம் = 3.53 ஆண்டுகள்
6% கூப்பன் வீதத்திற்கான கணக்கீடு
கூப்பன் கட்டணம் (சி) = 6% * $ 100,000 = $ 6,000
வகுத்தல் அல்லது பத்திரத்தின் விலை சூத்திரத்தைப் பயன்படுத்தி கணக்கிடப்படுகிறது,

- பத்திர விலை = 83,222.46
கால சூத்திரத்தின் எண்ணிக்கையின் கணக்கீடு பின்வருமாறு இருக்கும் -

= 302,100.95
எனவே, பத்திரத்தின் கால அளவீடு கீழே இருக்கும்,

காலம் = 302,100.95 / 83,222.46
- காலம் = 63 ஆண்டுகள்
கூப்பன் வீதத்திற்கான கணக்கீடு 4%
கூப்பன் கட்டணம் = 4% * $ 100,000 = $ 4,000
வகுத்தல் அல்லது பத்திரத்தின் விலை சூத்திரத்தைப் பயன்படுத்தி கணக்கிடப்படுகிறது,

- பத்திர விலை = 78,248.75
கால சூத்திரத்தின் எண்ணிக்கையின் கணக்கீடு பின்வருமாறு இருக்கும் -

= 292,469.09
எனவே, பத்திரத்தின் கால அளவீடு கீழே இருக்கும்,

கால ஃபார்முலா = 292,469.09 / 78,248.75
- காலம் = 3.74 ஆண்டுகள்
எடுத்துக்காட்டில் இருந்து, கூப்பன் வீதத்தின் குறைவுடன் ஒரு பத்திரத்தின் காலம் அதிகரிக்கிறது என்பதைக் காணலாம்.
கால சூத்திரத்தின் பொருத்தமும் பயன்பாடும்
வட்டி விகிதங்களில் ஏற்படும் மாற்றங்களுக்கு ஒரு பத்திரத்தின் உணர்திறனை சரிபார்க்க பத்திர முதலீட்டாளர்களால் பயன்படுத்தப்படுவதால் காலத்தின் கருத்தை புரிந்துகொள்வது முக்கியம். வட்டி விகிதத்தில் ஏற்பட்ட மாற்றத்தின் காரணமாக ஒரு பத்திரத்தின் சந்தை விலை எவ்வளவு மாறும் என்பதை ஒரு பத்திரத்தின் காலம் அடிப்படையில் குறிக்கிறது. வட்டி விகிதம் மற்றும் பத்திர விலை எதிர் திசைகளில் நகர்கின்றன என்பதையும், வட்டி விகிதம் வீழ்ச்சியடையும் போது பத்திர விலை உயர்வு போன்றவற்றையும் நினைவில் கொள்வது குறிப்பிடத்தக்கது.
வட்டி வீத வீழ்ச்சியிலிருந்து முதலீட்டாளர்கள் நன்மை பெற விரும்பினால், முதலீட்டாளர்கள் நீண்ட காலத்திற்கு பத்திரங்களை வாங்க விரும்புவர், இது குறைந்த கூப்பன் கட்டணம் மற்றும் நீண்ட முதிர்ச்சியுடன் பத்திரங்கள் இருந்தால் சாத்தியமாகும். மறுபுறம், வட்டி வீதத்தின் ஏற்ற இறக்கத்தைத் தவிர்க்க விரும்பும் முதலீட்டாளர்கள், முதலீட்டாளர்கள் குறைந்த கால அளவு அல்லது குறுகிய முதிர்வு மற்றும் அதிக கூப்பன் கொடுப்பனவுகளைக் கொண்ட பத்திரங்களில் முதலீடு செய்ய வேண்டும்.